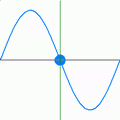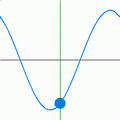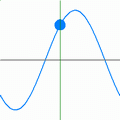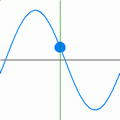
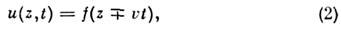Что такое плоская волна в физике
ПЛОСКАЯ ВОЛНА
— волна, ук-рой направление распространения одинаково во всех точках пространства. = v ф= v) существуют стационарные (т. е. перемещающиеся как целое) бегущиеП. в., к-рые можно представить в общем виде
Полезное
Смотреть что такое «ПЛОСКАЯ ВОЛНА» в других словарях:
плоская волна — Волна, фронт которой представляет собой плоскость, перпендикулярную к направлению распространения волны. [ГОСТ 24346 80] плоская волна 1. Волна с плоскими фронтами 2. Волна, в которой частицы с одной фазой лежат на плоских параллельных… … Справочник технического переводчика
плоская волна — Волны на поверхности океанов и морей, образующиеся из ветровых волн после полного прекращения воздействия на них ветра (обычно зыбь длиннее ветровых волн и более правильна). Syn.: зыбь … Словарь по географии
Плоская волна — 71. Плоская волна Волна, фронт которой представляет собой плоскость, перпендикулярную к направлению распространения волны Источник: ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
плоская волна — plokščioji banga statusas T sritis fizika atitikmenys: angl. plane wave vok. ebene Welle, f; flache Welle, f rus. плоская волна, f pranc. onde plane, f … Fizikos terminų žodynas
Плоская волна — волна, в которой всем точкам, лежащим в любой плоскости, перпендикулярной к направлению её распространения, в каждый момент соответствуют одинаковые смещения и скорости частиц среды (для механических волн) или одинаковые напряжённости… … Большая советская энциклопедия
ортогонализированная плоская волна — ortogonalizuotoji plokščioji banga statusas T sritis fizika atitikmenys: angl. orthogonalized plane wave vok. orthogonalisierte ebene Welle, f rus. ортогонализированная плоская волна, f pranc. onde plane orthogonalisée, f … Fizikos terminų žodynas
плоская радиоволна — плоская волна Поперечная радиоволна, поверхности равных фаз которой представляют собой параллельные плоскости, перпендикулярные к направлению распространения. [ГОСТ 24375 80] Тематики радиосвязь Обобщающие термины распространение радиоволн… … Справочник технического переводчика
Волна — У этого термина существуют и другие значения, см. Волна (значения). Волна изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами,… … Википедия
Плоская радиоволна — 46. Плоская радиоволна Плоская волна Источник: ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
плоская световая волна — Световая волна, фронт которой представляет собой плоскость. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики физическая оптика Обобщающие термины… … Справочник технического переводчика
Плоская волна
Другими решениями волнового уравнения являются сферическая волна ( концентрическая вокруг точки) и цилиндрическая волна (концентрическая вокруг прямой линии). Их можно легко аппроксимировать на небольших участках вдали от центра с помощью плоской волны.
Содержание
Однородная гармоническая плоская волна
Плоскую волну проще всего описать, если выбрать систему координат так, чтобы одна ось соответствовала направлению ее распространения. В направлениях, перпендикулярных распространению, не происходит колебаний. Таким образом, гармоничную однородную плоскую волну можно назвать
представляет собой плоское уравнение для волнового фронта.
Общая форма плоской волны
В общих чертах плоская волна описывается формулой
Плоская волна является решением волнового уравнения
На практике используются только гармонические плоские волны, поскольку любую общую плоскую волну можно представить как сумму гармонических плоских волн. Это связано с тем, что общую форму плоской волны A можно представить в виде интеграла Фурье :
Неоднородная плоская волна
Плоская волна всегда является решением уравнения Гельмгольца (временное преобразование Фурье волнового уравнения)
Чтобы уравнение Гельмгольца оставалось верным, волновое число должно оставаться действительным, что связано с условием k → ⋅ k → знак равно k 2 ( ω ) <\ displaystyle <\ vec
и означает ограничение на выбор комплексного волнового вектора. Это условие явно означает, что действительная часть ( ) волнового вектора должна быть перпендикулярна его мнимой части ( ). β → <\ displaystyle <\ vec <\ beta>>> 
поглощение
Если действительная и мнимая части комплексного волнового вектора выбраны как параллельные векторы, мнимая часть волнового числа не равна нулю, как в предыдущем разделе, и волновое число становится комплексным.
Уровни постоянной фазы и постоянной амплитуды идентичны, только амплитуда экспоненциально убывает в направлении распространения. Итак, это однородная плоская волна.
идеализация
Плоская волна всегда заполняет бесконечно протяженное пространство и поэтому является идеализацией реальной волны. Потому что, с одной стороны, плоская волна не может быть излучена конечно протяженным передатчиком, а с другой стороны, энергия плоской волны бесконечна. Оба они нефизичны.
Упругие волны (механические волны).
Возмущения, распространяющиеся в пространстве, удаляясь от места их возникновения, называют волнами.
Упругие волны — это возмущения, распространяющиеся в твердой, жидкой и газообразной средах благодаря действию в них сил упругости.
Сами эти среды называют упругими. Возмущение упругой среды — это любое отклонение частиц этой среды от своего положения равновесия.
Возьмем, например, длинную веревку (или резиновую трубку) и прикрепим один из ее концов к стене. Туго натянув веревку, резким боковым движением руки создадим на ее незакрепленном конце кратковременное возмущение. Мы увидим, что это возмущение побежит вдоль веревки и, дойдя до стены, отразится назад.
Начальное возмущение среды, приводящее к появлению в ней волны, вызывается действием в ней какого-нибудь инородного тела, которое называют источником волны. Это может быть рука человека, ударившего по веревке, камешек, упавший в воду, и т. д. Если действие источника носит кратковременный характер, то в среде возникает так называемая одиночная волна. Если же источник волны совершает длительное колебательное движение, то волны в среде начинают идти одна за другой. Подобную картину можно увидеть, поместив над ванной с водой вибрирующую пластину, имеющую наконечник, опущенный в воду.
Необходимым условием возникновения упругой волны является появление в момент возникновения возмущения сил упругости, препятствующих этому возмущению. Эти силы стремятся сблизить соседние частицы среды, если они расходятся, и отдалить их, когда они сближаются. Действуя на все более удаленные от источника частицы среды, силы упругости начинают выводить их из положения равновесия. Постепенно все частицы среды одна за другой вовлекаются в колебательное движение. Распространение этих колебаний и проявляется в виде волны.
В любой упругой среде одновременно существуют два вида движения: колебания частиц среды и распространение возмущения. Волна, в которой частицы среды колеблются вдоль направления ее распространения, называется продольной, а волна, в которой частицы среды колеблются поперек направления ее распространения, называется поперечной.
Продольная волна.
Волна, в которой колебания происходят вдоль направления распространения волны, называется продольной.
В упругой продольной волне возмущения представляют собой сжатия и разрежения среды. Деформация сжатия сопровождается возникновением сил упругости в любой среде. Поэтому продольные волны могут распространяться во всех средах (и в жидких, и в твердых, и в газообразных).
Пример распространения продольной упругой волны изображен на рисунке а и б выше. По левому концу длинной пружины, подвешенной на нитях, ударяют рукой. От удара несколько витков сближаются, возникает сила упругости, под действием которой эти витки начинают расходиться. Продолжая движение по инерции, они будут продолжать расходиться, минуя положение равновесия и образуя в этом месте разрежение (рисунок б). При ритмичном воздействии витки на конце пружины будут то сближаться, то отходить друг от друга, т. е. колебаться возле своего положения равновесия. Эти колебания постепенно передадутся от витка к витку вдоль всей пружины. По пружине распространятся сгущения и разрежения витков, или упругая волна.
Волны, в которых колебания происходят перпендикулярно направлению их распространения, называются поперечными. В поперечной упругой волне возмущения представляют собой смещения (сдвиги) одних слоев среды относительно других.
Деформация сдвига приводит к появлению сил упругости только в твердых телах: сдвиг слоев в газах и жидкостях возникновением сил упругости не сопровождается. Поэтому поперечные волны могут распространяться только в твердых телах.
Плоская волна — это волна, у которой направление распространения одинаково во всех точках пространства.
В такой волне амплитуда не меняется со временем (по мере удаления от источника). Получить такую волну можно, если большую пластину, находящуюся в сплошной однородной упругой среде, заставить колебаться перпендикулярно плоскости. Тогда все точки среды, примыкающей к пластине, будут колебаться с одинаковыми амплитудами и одинаковыми фазами. Распространяться эти колебания будут в виде воли в направлении нормали к пластине, причем все частицы среды, лежащие в плоскостях, параллельных пластине, будут колебаться с одинаковыми фазами.
Геометрическое место точек, в которых фаза колебаний имеет одно и то же значение, называется волновой поверхностью, или фронтом волны.
С этой точки зрения плоской волне можно дать и следующее определение:
Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.
Линия, нормальная к волновой поверхности, называется лучом. Вдоль лучей происходит перенос энергии волны. Для плоских волн лучи — это параллельные прямые.
Уравнение плоской синусоидальной волны имеет вид:
где s — смещение колеблющейся точки, sm — амплитуда колебаний, ω — циклическая частота, t — время, х — текущая координата, v — скорость распространения колебаний или скорость волны, φ0 — начальная фаза колебаний.
Сферической называется волна, волновые поверхности которой имеют вид концентрических сфер. Центр этих сфер называется центром волны.
Лучи в такой волне направлены вдоль радиусов, расходящихся от центра волны. На рисунке источником волны является пульсирующая сфера.
Амплитуда колебаний частиц в сферической волне обязательно убывает по мере удаления от источника. Энергия, излучаемая источником, равномерно распределяется по поверхности сферы, радиус которой непрерывно увеличивается по мере распространения волны. Уравнение сферической волны имеет вид:

Плоская волна
Смотреть что такое «Плоская волна» в других словарях:
ПЛОСКАЯ ВОЛНА — волна, у к рой направление распространения одинаково во всех точках пространства. Простейший пример однородная монохроматич. незатухающая П. в.: и(z, t)=Aeiwt±ikz, (1) где А амплитуда, j= wt±kz фаза, w=2p/Т круговая частота, Т период колебаний, k … Физическая энциклопедия
плоская волна — Волна, фронт которой представляет собой плоскость, перпендикулярную к направлению распространения волны. [ГОСТ 24346 80] плоская волна 1. Волна с плоскими фронтами 2. Волна, в которой частицы с одной фазой лежат на плоских параллельных… … Справочник технического переводчика
плоская волна — Волны на поверхности океанов и морей, образующиеся из ветровых волн после полного прекращения воздействия на них ветра (обычно зыбь длиннее ветровых волн и более правильна). Syn.: зыбь … Словарь по географии
Плоская волна — 71. Плоская волна Волна, фронт которой представляет собой плоскость, перпендикулярную к направлению распространения волны Источник: ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
плоская волна — plokščioji banga statusas T sritis fizika atitikmenys: angl. plane wave vok. ebene Welle, f; flache Welle, f rus. плоская волна, f pranc. onde plane, f … Fizikos terminų žodynas
ортогонализированная плоская волна — ortogonalizuotoji plokščioji banga statusas T sritis fizika atitikmenys: angl. orthogonalized plane wave vok. orthogonalisierte ebene Welle, f rus. ортогонализированная плоская волна, f pranc. onde plane orthogonalisée, f … Fizikos terminų žodynas
плоская радиоволна — плоская волна Поперечная радиоволна, поверхности равных фаз которой представляют собой параллельные плоскости, перпендикулярные к направлению распространения. [ГОСТ 24375 80] Тематики радиосвязь Обобщающие термины распространение радиоволн… … Справочник технического переводчика
Волна — У этого термина существуют и другие значения, см. Волна (значения). Волна изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами,… … Википедия
Плоская радиоволна — 46. Плоская радиоволна Плоская волна Источник: ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
плоская световая волна — Световая волна, фронт которой представляет собой плоскость. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики физическая оптика Обобщающие термины… … Справочник технического переводчика
Волны в физике — что это такое, виды, характеристики, примеры
Каждый день вас окружает множество волн. В этой статье вы узнаете, что это такое и какими свойствами они обладают.
Простое объяснение волн с точки зрения физики
В качестве концепции вы можете представить волну как форму с последовательными восходящими и нисходящими частями. К этой категории относится, например, волна воды.
Однако эти части, поднимающиеся и опускающиеся вверх и вниз, не являются случайными по форме и расположению, а следуют очень определенной схеме. Этот паттерн показывает, как частицы среды, в которой распространяется волна, колеблются вверх и вниз. Частицы «возмущаются» волной определенным образом.
Определение: под волной можно представить возмущение в среде, которое движется с фиксированной формой и постоянной скоростью.
На рисунке 1 показано, например, как такое возмущение в виде холма движется по веревке слева направо. Во время движения частицы веревки поднимаются вверх от переднего конца возмущения и тянутся вниз от заднего конца.

От света, который вам нужен, чтобы видеть, до звука, который вам нужен, чтобы слышать, до интернет-сигнала, который вам нужен для работы в Интернете, — все это волны. Как видите, волны — неотъемлемая часть жизни человека.
Виды волн
В этом подразделе мы рассмотрим различные виды волн и то, к какой области теоретической физики они относятся.
Поперечные и продольные волны
Например, в волне воды, которая движется слева направо, отдельные частицы воды колеблются вверх и вниз. Поэтому движение частиц перпендикулярно движению волны. Эти типы волн называются поперечными и могут быть поляризованными.
Звуковые волны (также называемые для краткости звуком), которые позволяют вам слышать, являются примером продольных волн. В продольных волнах частицы вовлеченной среды колеблются в направлении движения волны. Поэтому движение частиц параллельно движению волн.

Волны в физике
Следующий список дает вам представление о том, с какими волнами вам, возможно, придется иметь дело в той или иной области физики:
Волна — это тип возмущения, которое распространяется с фиксированной формой. В этом разделе мы рассмотрим его свойства и поведение. Мы рассмотрим следующие моменты немного подробнее:
Характеристики волн
Чтобы описать характеристики, рассмотрим частный случай синусоидальных волн. В синусоидальных волнах восходящие и нисходящие части повторяют форму синусоидальной кривой.
Из этой схемы (паттерна) (рисунок 3) мы выделили следующий фрагмент: кривая начинается с нуля, идет к самой низкой точке, затем возвращается к нулю, продолжается до самой высокой точки и, наконец, возвращается к нулю.

Амплитуда.
Расстояние по вертикали между высокой или низкой точкой и нулевой точкой называется амплитудой. Амплитуда обеспечивает барьер, внутри которого задерживаются восходящие и нисходящие части волны.
Например, если амплитуда водной волны составляет 2 метра, это означает, что при движении морской волны частицы воды поднимаются на максимальную высоту 2 метра.
Частота и длина волны.
Вы также можете представить себе синусоидальную волну следующим образом: мы копируем выбранный кусок и вставляем его бесконечное количество раз как слева, так и справа от него. Таким образом, этот выбранный фрагмент уже определяет поведение волны. Термин для этого — период.
Мы можем охарактеризовать этот период двумя способами:
Важно знать! Расстояние по горизонтали между двумя последовательными максимумами (самая высокая точка) или минимумом (самая низкая точка) часто называется длиной волны.

Скорость распространения волны.
Длина волны и частота волны тесно связаны между собой.
Важно знать! Скорость распространения волны = длина волны * частота волны.
Например, если вы раскачиваете веревку вверх и вниз, создавая «веревочную волну», скорость распространения говорит вам о том, как быстро удаляется от вас высокая точка (или любой другой участок) волны.
Отражение, преломление и дифракция волн.
Если волна попадает в другую среду, могут произойти следующие два явления:
Например, когда свет от солнца попадает на поверхность воды, среда меняется с воздуха на воду. Это приводит к тому, что часть света отражается, а часть преломляется. Это также является причиной того, что вы можете увидеть солнце, например, в луже воды.
Теперь для того, чтобы что-то произошло, волна не обязательно должна попасть на новый носитель. Если внутри текущей среды поместить препятствие, например, в виде стены с одним прямоугольным проходом, то может возникнуть явление дифракции (см. рисунок 5). Проще говоря, дифракция описывает явление, когда волна после прохождения не движется по прямой линии.

Суперпозиция волн.
До сих пор мы рассматривали только одну волну. Но что происходит, когда две (или более) волны сталкиваются? Возникает явление, которое называется суперпозицией волн. Однако эта суперпозиция не возникает каким-то образом, а следует определенному принципу, который мы знаем под названием «принцип суперпозиции».
Чтобы объяснить принцип суперпозиции в случае волн, давайте снова рассмотрим синусоидальные волны. Каждая точка на синусоиде дает вам значение, которое является мерой силы отклонения частиц.
Принцип суперпозиции простыми словами: в каждой точке пространства, где встречаются две волны, вы складываете значения двух синусоид. Итог этого сложения дает результирующую волну.
В соответствии с принципом суперпозиции различные явления могут наблюдаться в суперпозиции. К ним относятся, в частности:
Музыкальные инструменты создают стоячие волны посредством суперпозиции. Эти стоячие волны, в свою очередь, вибрируют в окружающем воздухе, создавая звуковые волны, которые доходят до ваших ушей и в конечном итоге позволяют вам услышать музыку.
Механические волны и электромагнитные волны
В этом разделе мы рассмотрим конкретные примеры механических и электромагнитных волн.
Механические волны
Волны, для распространения которых необходима среда, называются механическими волнами. Без среды механические волны не могут распространяться. В идеальном вакууме, например, звуковая волна не может распространяться.
Когда возникает механическая волна, периодическое движение одной частицы среды передается соседним частицам по мере того, как волна движется через среду. Частицы определенным образом «механически» связаны друг с другом.
Самым важным примером механической волны является звук. Звук окружает вас каждый день, будь то разговор с друзьями или прослушивание музыки. Звуковые волны позволяют вам слышать. Они возникают в результате вибрации частиц воздуха.
Электромагнитные волны
Электромагнитные волны не нуждаются в среде для распространения. Если для их распространения не нужна среда, то что тогда колеблется? Электромагнитная волна состоит из электрического и магнитного полей. И именно эти поля колеблются вверх и вниз.
Помните! Периодически изменяющееся электрическое поле приводит к возникновению магнитного поля, которое также периодически изменяется, и наоборот, — таким образом происходит генерация электромагнитной волны.
Например, свет солнца — это электромагнитная волна. Это означает, что электромагнитные волны, помимо всего прочего, отвечают за то, что вы можете что-то видеть. Но вам также нужны электромагнитные волны, чтобы иметь возможность совершать телефонные звонки или пользоваться Интернетом.