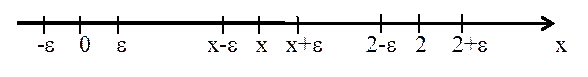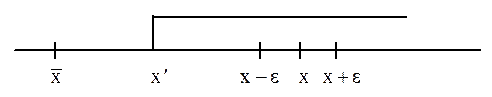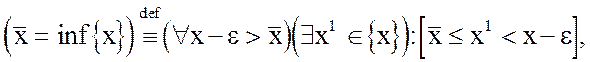Что такое предельная точка последовательности

Математический анализ
Записки лекций

Илья Щуров (НИУ ВШЭ)

9 Подпоследовательности, предельные точки и теорема Больцано — Вейерштрасса

9.1 Подпоследовательности и предельные точки

9.1.1 Подпоследовательности

Доказательство первых двух пунктов этого утверждения простое и я советую его провести самостоятельно. Третий пункт вынесен в качестве задачи на семинары. Обратное неверно: если подпоследовательность обладает каким-нибудь из этих свойств (скажем, ограничена), это ничего не говорит про аналогичное свойство исходной последовательности (приведите примеры).

Неверный ответ. Попробуйте доказать 🙂

9.1.2 Предельные точки

При решении некоторых задач удобным оказывается другое определение предельной точки.

Сравните это определение с определением предела — в чём ключевое различие?

Есть ли последовательности, не имеющие предельных точек? Тут легко привести пример — скажем, последовательность a n = n обладает таким свойством: она посещает каждое натуральное число ровно один раз, а потом уходит от него на расстояние как минимум 1.

Заметим, что последовательсноть a n = n неограничена. Бывают ли ограниченные последовательности без предельных точек? Прежде, чем читать дальше, попробуйте придумать такую.

9.2 Теорема Больцано — Вейерштрасса

Для доказательства этой теоремы нам понадобится вспомогательная лемма, которая представляет и самостоятельный интерес — она пригодится нам ещё несколько раз.

9.2.1 Лемма о вложенных отрезках

Потребуем также, чтобы длины отрезков стремились к нулю:

Неверный ответ. Какие же это?

9.2.2 Деление отрезка пополам

Источник

Предельные точки, верхний и нижний пределы последовательности

Предельные точки, верхний и нижний пределы последовательности

Давайте сначала докажем это утверждение до 1°. Зафиксируйте любое Людмила Фирмаль

положительное число e, используйте сходимость последовательностидля ограничения a и выберите число N этого e так, чтобы|CP—a / ) бесконечной прямой называется точкой последовательности. Давайте убедимся, что определения 1 и 2 эквивалентны. 1) окрестность e x содержит бесконечно много элементов последовательности. Рассмотрим множество e-окружностей точки X. 1 Лл»»» • • • ‘» > • • • • 2 3 П В первой из этих областей выделяют элементы последовательности xy1 из нескольких кг,во второй из этих областей-элементы последовательности x*2 из

последовательностис бесконечным числом точек разрыва. Выше (Глава 3, Глава 7, Раздел 2) мы установили, что множество всех рациональных чисел из отрезка[0,1]может быть пронумеровано в последовательности. Докажите, что любой вещественный x из отрезка [0,1]является точкой разрыва данной последовательности. Заметим, что даже если число сегментов[0,1]x равно 0 О п р ЕД е л я Е4. Минимальная точка поля последовательностиназывается самой нижней точкой этой последовательности, обозначаемой символом x=PT CP. п — > Возникает вопрос о существовании хотя бы одного предела и верхнего и нижнего пределов любого ограниченного массива.96

канал 3. Теория пределов Следующие замечательные теоремы справедливы. О С Н О В Н А я т е О Р Е М А3. 16. Все граничные последовательности имеют верхний и нижний предел, особенно по крайней мере одну предельную точку. Д О К а з а т е л ь с т в о. рассмотрим доказательство существования хотя бы одной предельной точки и верхнего предела любого ограниченного массива. (Существование нижнего предела было доказано как well.It является ограниченным массивом произвольных. Из-за условия ограничения существуют два действительных числа PG и M, так что любой элемент последовательности XPудовлетворяет неравенству t^XPсправа*,

или такие элементы являются просто конечным числом. * Напомним, что термин «Y находится справа от x» означает, что x n y связано неравенством y>x. Другими словами, действительное число x принадлежит множеству, если правая часть x не превышает конечного числа последовательностейи не принадлежит множеству, а правая часть этого числа x является числом последовательностей. Заметим, что множество, конечно, не пусто: оно принадлежит любому вещественному числу x, удовлетворяющему неравенству x>L1 (точка последовательностисправа от такого x, далее ясно, что множествоможет иметь границу снизу, а любое число, меньшее t, может быть взято в качестве нижней стороны (число, если вы хотите, чтобы оно было Согласно основной теореме главы 2.1, множествоимеет точную нижнюю границу, обозначаемую символом X.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Предельные точки последовательности. Числовая прямая

По этой ссылке вы найдёте полный курс лекций по математике:

Поэтому достаточно очевидно следующее утверждение. Утверждение б.б. Если lim = 6 6 R, то b — единственная предельная точка последовательности <хп>. Действительно, в силу определения 6.3 предела последовательности все ее элементы начиная с некоторого номера попадают в любую сколь угодно малую окрестность точки 6, а потому в окрестность никакой другой точки не могут попасть элементы с произвольно большими номерами.

Следовательно, условие определения 6.7 выполнимо лишь для единственной точки 6. Однако не всякая предельная точка (иногда ее называют тонкой сгущенил) последовательности является ее пределом. Так, последовательность (б.б) не имеет предела (см. пример 6.5), но имеет две предельные точки х = 1 и х = — 1. Последовательность <(-1)пп>в качестве предельных имеет две бесконечные точки +оо и —со расширенной числовой прямой, объединение которых обозначают одним символом оо.

Очевидно, что если имеет пределом число 6, то любая ее подпоследовательность имеет тот же самый предел, поскольку начиная с некоторого номера все элементы как исходной последовательности, так и любой ее подпоследовательности попадают в любую выбранную окрестность точки 6. В то же время любая предельная точка подпоследовательности является предельной и для последовательности. Теорема в.9. Из любой последовательности, имеющей предельную точку, можно выбрать подпоследовательность, имеющую своим пределом эту предельную’точку. Пусть b — предельная точка последовательности <хп>.

Теорема 8.10. Если некоторая последовательность имеет подпоследовательность с пределом 6, то Ь есть предельная точка этой последовательности. Из определения 6.3 предела последовательности следует, что начиная с некоторого номера все элементы подпоследовательности с пределом b попадают в окрестность U(b, е) произвольного радиуса е. Поскольку элементы подпоследовательности являются одновременно элементами последовательности <хп>> внутрь этой окрестности попадают элементы хп со сколь угодно большими номерами, а это в силу определения 6.7 означает, что Ь — предельная точка последовательности <яп>.

Возможно вам будут полезны данные страницы:

Замечание 0.2. Теоремы 6.9 и 6.10 справедливы и в случае, когда предельная точка является бесконечной, если при доказательстве вмерто окрестности U(6, 1 /п) рассматривать окрестность (или окрестности Условие, при котором из последовательности можно выделить сходящуюся подпоследовательность, устанавливает следующая теорема. Теорема 6.11 (Больцано — Веиерштрасса). Всякая ограниченная последовательность содержит подпоследовательность, сходящуюся к конечному пределу.

Пусть все элементы последовательности <ап>заключены между числами а и 6, т.е. хп € [а, b] Vn € N. Разделим отрезок [а, Ь] пополам. Тогда хотя бы одна из его половин будет содержать бесконечное множество элементов последовательности, так как в противном случае и весь отрезок [а, Ь] содержал бы конечное их число, что невозможно. Пусть ] будет та из половин отрезка [а, 6], которая содержит бесконечное множество элементов последовательности <жп>(или если обе половины таковы, то любая из них). Аналогично из отрезка [ai, b<\ выделим его половину [a2) 62], содержащую бесконечное множество элементов последовательности, и т.д.

Согласно определению 6.7 х — предельная точка этой последовательности. Тогда в силу теоремы 6.9 существует подпоследовательность, сходящаяся к точке х. Метод рассуждений, использованный при доказательстве этой теоремы (ее иногда называют леммой Больцано — Вейер-штрасса) и связанный с последовательным делением пополам рассматриваемых отрезков, известен под названием метода Больцано. Эта теорема значительно упрощает доказательство многих сложных теорем.

Она позволяет доказать иным (иногда более простым) путем ряд ключевых теорем.

Дополнение 6.2. Доказательство признака Вейерштрасса и критерия Коши Сначала докажем утверждение 6.1 (признак Вейерштрасса сходимости ограниченной монотонной последовательности). Предположим, что последовательность <яп>неубывающая. Тогда множество ее значений ограничено сверху и по теореме 2.1 имеет точную верхнюю граньу которую обозначим sup be R. В силу свойств точной верхней грани (см. 2.7) Предельные точки последовательности числовая прямая Доказательство признака Вейерштрасса и критерия Коши.

Согласно определению 6.1 для неубывающей последовательности имеем или Тогда > Ny а с учетом (6.34) получим что соответствует определению 6.3 предела последовательности, т.е. 31im и lim = 66R. Если последовательность <хп>невозрастающая, то ход доказательства аналогичен. Теперь перейдем к доказательству достаточности критерия Кохии сходимости последовательности (см. утверждение 6.3), поскольку необходимость условия критерия следует из теоремы 6.7.

Обозначим ее через Ь. Таким образом, при Из сравнения (6.36) и (6.37) в итоге получим что соответствует определению 6.3 предела последовательности, т.е. 31im и lim = 6 6 R. Фундаментальные последовательности начал изучать Боль-цано. Но он не располагал строгой теорией действительных чисел, и поэтому ему не удалось доказать сходимость фундаментальной последовательности. Это сделал Коши, приняв за очевидное принцип вложенных отрезков, который позднее обосновал Кантор.

Имя Коши получил не только критерий сходимости последовательности, но и фундаментальную последовательность часто именуют последовательностью Коши, а имя Кантора носит принцип вложенных отрезков. Вопросы и задачи 8.1. Доказать, что: 6.2. Привести примеры несходящихся последовательностей с элементами, принадлежащими множествам Q и R\Q. 0.3. При каких условиях члены арифметической и геометрической прогрессий образуют убывающую и возрастающую последовательности? 6.4. Доказать соотношения, которые следуют из табл. 6.1. 6.5.

Являются ли монотонными последовательности <-хп>, <1>и <х£>, если последовательность <хп>возрастающая? Могут ли быть первые три последовательности монотонными, если последовательность <хп>немонотонная? в.14. Доказать, что если сходящаяся последовательность <хп>возрастает, то lim = sup. 6.15. Пусть <хп>и <уп>— возрастающие последовательности и Vn 6 N х„ ^ уп. Доказать, что: Предельные точки последовательности числовая прямая.

и критерия Коши. 1) если <уп>сходится, то и <хп>сходится; 2) если <хп>расходится, то и <уп>расходится. 6.16. Доказать, что существует единственная точка г, принадлежащая любому из отрезков, левым концом которого является элемент возрастающей последовательности <яп>, а правым — элемент с тем же номером убывающей последовательности <уп>> причем уп-£п-»0 при п-»оо. в.17.

Последовательности <хп>и <уп>определены заданием элементов х\ и у\ при условии 0 и рекуррентными формулами хп+1 = (хп + уп)/2 и Уп+1 = 2хпуп/(х п «Ь Уп)* Доказать, что эти последовательности строго монотонные и сходятся к одному и тому же пределу. Найти этот предел. в.18. Доказать сходимость и вычислить предел последовательностей: 6.19. Привести примеры последовательностей, не являющихся фундаментальными. 6.20.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Предельные точки последовательности

Лемма 1.Если x- предельная точка последовательности k>, то из этой последовательности можно выделить подпоследовательность n_k>, сходящуюся к числу x.

Из леммы 1 следует, что можно дать другое определение предельной точки последовательности, эквивалентное определению 1.

Определение 2. Точка x бесконечно прямой называется предельной точкой последовательности k>, если из этой последовательности можно выделить подпоследовательность, сходящуюся к x.

Лемма 2.Каждая сходящаяся последовательность имеет только одну предельную точку, совпадающую с пределом этой последовательности.

Замечание.Если последовательность сходится, то она в силу леммы 2 имеет только одну предельную точку. Однако, если n> не является сходящейся, то она может иметь несколько предельных точек (и, вообще бесконечно много предельных точек). Покажем, например, что <1+(-1) n >имеет две предельные точки.

Теорема.У всякой ограниченной последовательности существует хотя бы одна предельная точка.

Пусть x- любое число, превосходящее 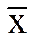. Выберем e>0 настолько малым,

что x-e>.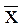

и x 1 Î, правее x 1 лежит конечное число элементов последовательности n> или их вовсе нет, т.е. x не является предельной точкой последовательности n>.

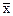
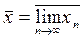
Определение.Наибольшая предельная точка последовательности n> называется верхним пределом последовательности и обозначается символом . Из замечания следует, что у всякой ограниченной последовательности есть верхний предел.

Аналогично вводится понятие нижнего предела 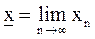(как наименьшей предельной точки последовательности n>).

Итак, мы доказали следующее утверждение. У всякой ограниченной последовательности существует верхний и нижний пределы.

Сформулируем без доказательства следующую теорему.

Теорема.Для того, чтобы последовательность 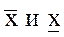n> была сходящейся, необходимо и достаточно, чтобы она была ограниченной и чтобы ее верхний и нижний пределы совпадали.

Результаты этого пункта приводят к следующей основной теореме Больцано-Вейерштрасса.

Теорема Больцано-Вейерштрасса.Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Доказательство. Так как последовательность n> ограничена, то она имеет хотя бы одну предельную точку x. Тогда из этой последовательности можно выделить подпоследовательность, сходящуюся к точке x (следует из определения 2 предельной точки).

Замечание.Из любой ограниченной последовательности можно выделить монотонную сходящуюся последовательность.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

2. Предел последовательности

Последовательность

Таким образом, числовая последовательность это частный вид функции, в котором элементу из множества натуральных чисел по определенному закону однозначно ставится в соответствие элемент из множества вещественных чисел.

Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.

Пример. Последовательность простых чисел является подпоследовательностью последовательности натуральных чисел. Последовательность натуральных чисел, кратных 12, является подпоследовательностью последовательности чётных натуральных чисел.

Определение. Стационарная последовательность — это последовательность, все члены которой, начиная с некоторого, равны.

Определение. Ограниченная сверху последовательность — это последовательность элементов множества X, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.

Ограниченная снизу последовательность — это последовательность элементов множества X, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.

Ограниченная последовательность — это последовательность, ограниченная и сверху, и снизу.

Геометрически ограниченность последовательности означает, что все члены последовательности содержатся в С-окрестности точки нуль.

Проколотой окрестностью точки называется окрестность точки, из которой исключена эта точка.

Предел последовательности

\exists N(\varepsilon )\in \mathbb \colon

\exists N(E)\in \mathbb \colon

\forall n\geqslant N\Rightarrow |x_|>E$$

Любая последовательность, стремящаяся к бесконечности — неограниченная. Однако обратное неверно.

В самом общем случае у произвольной последовательности может быть от нуля до бесконечного числа различных частичных пределов. При этом, если обычный предел характеризует точку, к которой элементы последовательности приближаются с ростом номера, то частичные пределы характеризуют точки, вблизи которых лежит бесконечно много элементов последовательности.

Верхний (lim sup) и нижний пределы (lim inf):

Свойства

Сумма, разность, произведение сходящихся последовательностей также является сходящейся последовательностью. [Частное не всегда]

Взятие предела числовой последовательности является линейным:

Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует.

Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.

Единственность. Сходящаяся числовая последовательность имеет только один предел. Доказательство: Тер-Крикоров, с.40.

Замкнутость. Если все элементы сходящейся числовой последовательности лежат на некотором отрезке, то на этом же отрезке лежит и её предел.

У возрастающей ограниченной сверху последовательности есть предел. То же верно для убывающей ограниченной снизу последовательности.

Предел средних арифметических, геометрических

Тем самым, операция взятия среднего обладает свойством регулярности — сохраняет свойство сходимости последовательности и её предел.

Аналогично для последовательности средних геометрических, доказательство

Предельный переход в неравенствах

Доказательство от противного, по определению предела.

Предельный переход сохраняет знак нестрогого неравенства. Однако знак строгого неравенства, вообще говоря, не сохраняется.

Теорема о двух милиционерах

Справедлива теорема о двух милиционерах (теорема сжатия)

\forall n\geqslant N\colon x_\leqslant z_\leqslant y_

Бесконечно малые

Бесконечно малая последовательность — это последовательность, предел которой равен нулю.

Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности. [если для любого вещественного числа все члены последовательности, начиная с некоторого, оказываются по модулю больше этого числа. ]

Сумма, разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

Любая бесконечно малая последовательность ограничена.

Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.

Предельная точка последовательности

Определение. Назовем точку x предельной точкой множества E, если в произвольной окрестности точки x существует хотя бы одна точка из E, отличная от x.

Сама точка x может принадлежать, а может и не принадлежать множеству E.

$$\forall \varepsilon > 0 \, \exists y, y \ne x : \, |x-y| 0

\exists X\subseteq \mathbb \colon \left|X\right|=\aleph _<0>\land \forall i\in X\colon \left|x_-x\right| 0

\exists x \in X\colon \, 0 0$ с центром в x нет ни одной точки из E, отличной от x, а это невозможно, поскольку x – предельная точка множества E.

Теорема. Точка является предельной точкой последовательности тогда и только тогда, когда из этой последовательности можно выделить подпоследовательность, сходящуюся к этой точке.

Задача. Доказать, что если последовательность сходится к a (то есть a является ее пределом), то она не имеет предельных точек, отличных от a.

т.е. Всякая сходящаяся числовая последовательность имеет только одну предельную точку.

Для сходящихся числовых последовательностей предельная точка совпадает с пределом.

У произвольной числовой последовательности имеется хотя бы одна предельная точка (либо вещественная, либо бесконечность).

Пример. У последовательности из всех рациональных чисел, занумерованных произвольным образом, существует бесконечно много предельных точек.

Примеры

Фундаментальная последовательность

Определение. Фундаментальная последовательность, или сходящаяся в себе последовательность, или последовательность Коши — последовательность точек метрического пространства такая, что для любого заданного расстояния существует элемент последовательности, начиная с которого все элементы последовательности находятся друг от друга на расстоянии менее, чем заданное.

Определение. Фундаментальная последовательность — это последовательность элементов метрического пространства, в которой для любого наперёд заданного расстояния найдётся такой элемент, расстояние от которого до любого из следующих за ним элементов не превышает заданного.

Для числовых последовательностей понятия фундаментальной и сходящейся последовательностей эквивалентны, однако в общем случае это не так.

Всякая сходящаяся последовательность является фундаментальной. При этом фундаментальная числовая последовательность всегда сходится (как и любая фундаментальная последовательность элементов полного пространства).

Определение. Пространство, в котором каждая фундаментальная последовательность сходится к элементу этого же пространства, называется полным.

Каждая сходящаяся последовательность является фундаментальной, но не каждая фундаментальная последовательность сходится к элементу из своего пространства.

Метрическое пространство является полным тогда и только тогда, когда всякая система вложенных замкнутых шаров с неограниченно убывающим радиусом имеет непустое пересечение, состоящее из одной точки.

Теорема Больцано — Вейерштрасса

Теорема. Если последовательность имеет предел, то она ограничена. [очевидно. например, взять ε=1]

Ограниченная последовательность имеет по крайней мере одну предельную точку.

Теорема Больцано — Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Источник