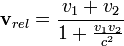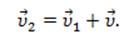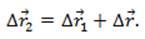Что такое сложение скоростей
Правило сложения скоростей
При рассмотрении сложного движения (то есть когда точка или тело движутся в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.
Содержание
Классическая механика
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.
Примеры
Релятивистская механика
В XIX веке классическая механика столкнулась с проблемой распространение этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики, перенесёнными в новую область электромагнитных процессов.
Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).
Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе осчёта — всегда равно их расстоянию в другой инерциальной системе.
Вторая идея — принцип относительности. Находясь на корабле, движущимся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое электродинамическими эффектами? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразованиям. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.
Теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Правило сложение скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:
Можно заметить, что в случае, когда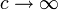 
, преобразования Лоренца переходят в преобразования Галилея. То же самое происходит в случае, когда 
. Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона либо в мире с бесконечной скоростью света, либо при скоростях, малых по сравнению со скоростью света. Последнее объясняет, каким образом сочетаются эти две теории — первая является уточнением второй.
Сложение скоростей
При рассмотрении сложного движения (то есть когда точка или тело движется в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.
Содержание
Классическая механика
Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.
Примеры
Релятивистская механика
В XIX веке классическая механика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики, перенесёнными в новую область электромагнитных процессов.
Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).
Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе осчёта — всегда равно их расстоянию в другой инерциальной системе.
Вторая идея — принцип относительности. Находясь на корабле, движущимся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое электродинамическими эффектами? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразованиям. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.
Теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Правило сложение скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:
Можно заметить, что в случае, когда 
, преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом сочетаются эти две теории — первая является уточнением второй.
Кинематика. Сложение скоростей.
С помощью закона сложения скоростей определяется скорость материальной точки относительно неподвижной системы отсчета. Она равна сумме скорости точки относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы:
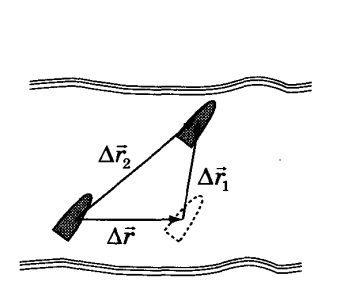
Рассмотрим движение одного и того же тела относительно двух тел отсчета, движущихся друг относительно друга. Для простоты допустим, что одно из тел отсчета неподвижно, а второе движется относительно первого прямолинейно и равномерно.
Лодка плывет со скоростью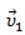 
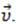
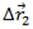
по реке (система отсчета К1). За неподвижное тело примем берег (система отсчета К2), а за подвижное – воду и обозначим скорость ее движения относительно берега через 
Векторы перемещений лодки относительно воды 
, реки относительно берега 
и суммарный вектор перемещения лодки относительно берега 
изображены на рисунке. Математически это можно выразить уравнением:
Поделив обе части уравнения на Δt, мы получим:
что равносильно первому уравнению.
Вместо векторов воспользовавшись их проекциями на оси координат, получим:
Проекции скоростей складываем алгебраически.
Закон сложения скоростей
Закон сложения скоростей — что это такое
В классической механике применяют термин, который звучит, как абсолютная скорость точки. Данная величина является суммой двух векторов: относительная и переносная скорости точки. В подобном равенстве выражена теорема сложения скоростей. Общепринятым положением является равенство скорости движения какого-либо объекта в рамках неподвижной системы отсчета и векторной суммы скорости аналогичного физического тела в условиях относительно подвижной системы отсчета. Данными координатами определяется непосредственное нахождение тела.
Классический закон сложения скоростей определяет, что скорость тела относительно неподвижной системы отсчета представляет собой геометрическую сумму двух скоростей, включая скорость тела относительно подвижной системы отсчета и скорость подвижной системы отсчета относительно неподвижной.
Классический вид, формула расчета
Релятивистским законом сложения скоростей являются соотношения, справедливые для частицы, перемещающейся параллельно относительной скорости систем отсчета:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Соотношение теории имеет следующий вид:
В случае, когда u \(u_
Преобразование координат и времени
Спустя какой-то небольшой промежуток времени \(\Delta t^<,>\) частица переместилась в точку:
Таким образом, при движении частицы происходят два события. Можно записать следующую формулу:
где \( \Delta v^<,>_
Уравнения будут иметь следующий вид:
\(\Delta x=\Delta x^<,>+V\Delta t^<,>\)
Исходя из составленных формул можно сделать вывод о том, что компоненты скорости той же частицы в системе \(К\) будут записаны следующим образом:
Уравнение представляет собой закон сложения скоростей. Данную закономерность можно привести в векторный вид:
Координаты в системе \(К\) и системе \(K^<,>\) будут параллельны.
Алгоритм решения задач
Существуют правила, которые являются основой механической физики. Исходя из данных соотношений, можно рассмотреть примеры сложения скоростей. Простейшими объектами для объяснения физических законов являются, к примеру, человек и любой перемещающийся в пространстве объект, с которым он прямо или косвенно взаимодействует.
Пример
Можно представить, что человек совершает прямолинейное движение вдоль коридора пассажирского поезда со скоростью пять километров в час. При этом равномерная скорость состава составляет 100 километров в час. Скорость человека, относительно пространства, которое его окружает, будет равна 105 километрам в час. Следует учитывать одинаковое направление перемещения человека и поезда.
В случае, когда направления движения человека и транспорта противоположны, данный принцип также справедлив. Тогда человек будет двигаться относительно окружающего пространства со скоростью 95 километров в час.
При рассмотрении объектов, скорости которых равны, можно сделать вывод, что относительно друг друга они неподвижны. Во время вращения скорость рассматриваемого тела представляет собой совокупность скоростей перемещения тела относительно движущейся поверхности другого объекта.
Решение задач на сложение скоростей выполняется в несколько этапов:
Задача 1
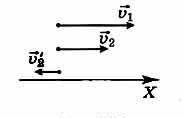
На примере рассмотрено равномерное движение двух поездов друг за другом. Первый поезд перемещается со скоростью 80 км/ч, а второй — 60 км/ч. Требуется рассчитать, какова скорость второго поезда относительно первого.
Решение
Следует обозначить скорость первого транспортного средства по отношению к земле с помощью \(\vec
Тогда скорость второго поезда составит \(\vec
Исходя из закона сложения скоростей:
где \(\vec
Такой метод сложения скоростей наглядно представлен на рисунке. Схематично скорость второго поезда по отношению к первому направлена противоположно направлению перемещения поездов, и можно наблюдать удаление второго поезда от первого. Проекция скорости \(\vec
Задача 2
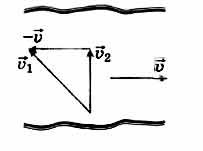
Река течет со скоростью \(v = 1,5\) м/с. Требуется определить модуль скорости \(v_<1>\) по отношению к воде. Необходимо учитывать, что в случае движения катера перпендикулярно относительно берега, его скорость составляет \(v_<2>=2\) м/с.
Решение
Исходя из закона сложения скоростей:
Формула для расчета скорости катера относительно реки:
Векторное сложение скоростей представлено на рисунке. На схеме получаем треугольник скоростей с прямым углом, поэтому:
Ответ: модуль скорости \(v_<1>\) по отношению к воде составляет \(2,5\) м/с.
Задача 3
Скорость движения самолета относительно воздуха составляет 300 км/ч. Объект движется в северном направлении. При возникновении северо-западного ветра, скорость которого 100 км/ч по отношению к земле, самолет должен сохранить исходное направление. Требуется рассчитать угол, под которым летчик удерживает направление самолета для продолжения пути на север, а также скорость самолета относительно земли.
Решение
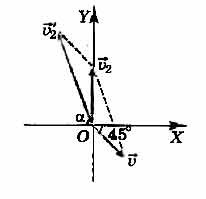
Необходимо связать неподвижную систему отсчета с землей, а подвижную — с воздухом. Скорость самолета по отношению к земле можно рассчитать, как сумму скорости самолета относительно воздуха и скорость ветра относительно земли. В таком случае, исходя из закона сложения скоростей:
Рисунок демонстрирует направление этих скоростей. Направление скоростей выполнено таким образом, чтобы проекции скорости самолёта относительно ветра и скорости ветра на оси ОХ равнялись по модулю и были направлены противоположно:
Если рассматривать проекцию на ось ОУ, то уравнение примет такой вид:
В таком случае, искомая скорость самолета составит:
Данное равенство позволит определить угол α:
Подставив числовые характеристики, получим:
Найти \(\sin \alpha\) можно таким образом:
Скорость самолета относительно земли составит:
Ответ: угол, под которым летчик удерживает направление самолета для продолжения пути на север, равен \(76^<0>\) ; скорость самолета относительно земли примерно равна 220 км/ч.
Что такое сложение скоростей
Формулировка закона:
Как в учебнике Буховцева для 10 класса:
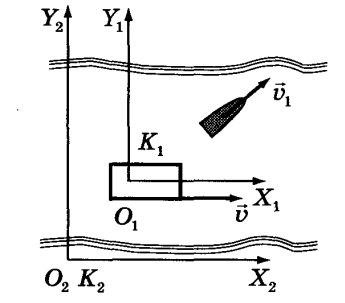
Если тело движется относительно системы отсчета К1 со скоростью V1,
а сама система отсчета К1 движется относительно другой системы отсчета К2 со скоростью V,
то скорость тела (V2) относительно второй системы отсчета К2
равна геометрической сумме векторов V1 и V.
Упрощаем форммулировку, не меняя смысла:
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета.
Вторая формулировка запоминается проще, какой ползоваться решайте сами!
Алгоритм решения задачи на закон сложения скоростей
Если вы внимательно прочитали пояснения к формуле, то решение любой задачи, пойдет «на автомате»!
P.S. В условиях задачи скорости тел заданы обычно относительно неподвижной системы отсчета (например, дороги или берега)
3. Ввести обозначения скоростей (V1, V2, V).
4. Сделать чертеж, на котором показать координатную ось ОХ и векторы скорости.
Лучше, если ОХ будет совпадать по направлению с вектором скорости выбранного тела.
5. Записать формулу закона сложения скоростей в векторном виде.
6. Выразить из формулы искомую скорость в векторном виде.
7. Выразить искомую скорость в проекциях.
8. Определить по чертежу знаки проекций.
9. Расчет в проекциях.
10. В ответе не забыть перейти от проекции к модулю.
Пример решения простейшей задачи на закон сложения скоростей
Задача
Два автомобиля движутся равномерно по шоссе навстречу друг другу. Модули их скоростей равны 10 м/с и 20 м/с.
Определить скорость первого автомобиля относительно второго.
Решение:
Еще раз! Если вы внимательно прочитали пояснения к формуле, то решение любой задачи, пойдет «на автомате»!
Теперь понятно, что в задаче надо определить V1.
4. Делаем чертеж, выписываем формулу: