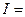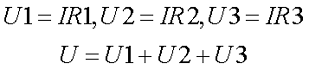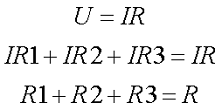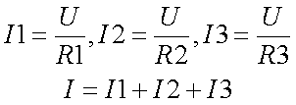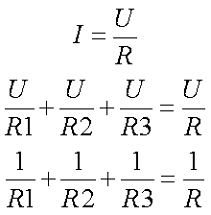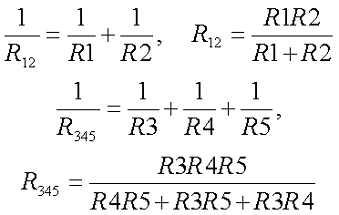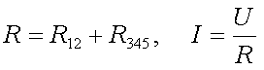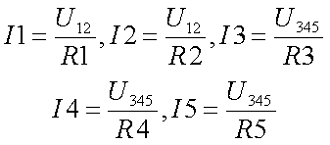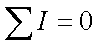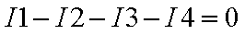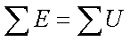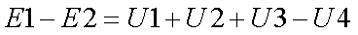Смешанные электрические цепи

Вы будете перенаправлены на Автор24

Смешанным соединением элементов называют всевозможные сочетания последовательной и параллельной разновидностей соединений. В такой цепи возможно различное количество узлов и ветвей.

Электрическая цепь со смешанным соединением элементов

Смешанным считают такое соединение, при котором в цепи существуют группы сопротивлений, включенных параллельно и последовательно.

$R_ = R_3 + R_cd = R+\frac<2>$

Смешанное соединение и сложные электрические цепи

Частым явлением в электрических цепях считается соединение смешанного типа (то есть комбинирование параллельного и последовательного соединений).

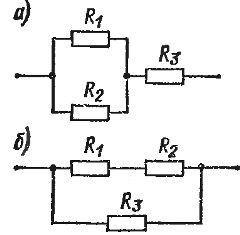
Если, например, взять 3 прибора, то возможными будут два варианта смешанного соединения. В первом случае мы наблюдаем соединение двух приборов параллельным образом при последовательном подключении к ним третьего.

При условии большего количества приборов, схемы смешанного соединения будут более сложными. Иногда встречаются также усложненные цепи, содержащие несколько ЭДС-источников.

Для расчета сложных цепей применяются различные методики. Наиболее распространенной считается методика, основанная на применении второго закона Кирхгофа. В наиболее общем формате закон сформулирован таким образом: в каком-либо замкнутом контуре алгебраическая сумма ЭДС будет равнозначной такого же типа сумме падений напряжений.

Алгебраическая сумма берется по той причине, что ЭДС, действующие встречным образом в отношении друг друга, или созданные противоположно направленными токами напряжения будут иметь разные знаки.

Готовые работы на аналогичную тему

При расчетах сложной цепи в большинстве примеров бывают известными сопротивления отдельных участков цепи и ЭДС, включенных источников. Для нахождения токов следует (на основе второго закона Кирхгофа) составить уравнения (для замкнутых контуров), в которых токи будут считаться неизвестными величинами.

К таким уравнениям также добавляются уравнения для точек разветвления, составленные по принципу первого закона Кирхгофа. При решении такой системы уравнений определяются токи. В случае с более сложными цепями, подобный метод будет достаточно громоздким, что обусловлено наличием большого числа неизвестных.

Смешанное соединение резисторов

Резистор считается устройством со стабильным значением сопротивления, что позволяет производить регулирование параметров на любых участках электроцепи. Существуют определенные разновидности соединений, к которым, в том числе, будет относиться и соединение смешанного типа для резисторов.

От применения определенного способа в конкретной схеме будет зависеть показатель неустойчивости напряжения (падение напряжения), а также распределение токов в цепи. Вариант смешанного соединения состоит из подключений последовательного и параллельного видов активных сопротивлений. Это объясняет необходимость первоочередного рассмотрения этих двух типов соединений для понимания работы других схем.

Схеме смешанного соединения будут присущи свойства схем последовательного и параллельного соединений резисторов. В таком случае элементы будут частично подключены последовательным способом, а частично – параллельным.

В заключение важно отметить присущие смешанному типу соединения резисторов положительные и отрицательные качества последовательного и параллельного соединений. Такое свойство успешно применяется на практике с электрическими схемами.

Источник

Смешанное соединение элементов.

Смешанным соединением элементов называют все возможные

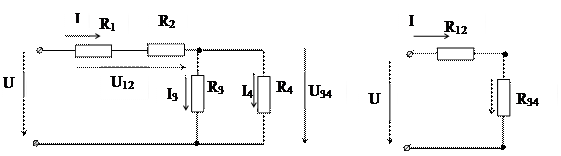
сочетания последовательного и параллельного соединений. В такой цепи может быть различное число узлов и ветвей. Один из примеров смешанного соединения представлен на схеме (рис. 1.3, а).

Рис.1.3 Схема смешанного соединения элементов (а) и ее эквивалентные схемы (б, в)

Для расчета такой схемы необходимо сначала определить эквивалентные сопротивления тех частей схемы, которые представляют собой только последовательное или только параллельное соединение. В предложенной схеме элементы R₁иR₂соединены между собой последовательно, а элементы R₃иR₄ – параллельно. Используя приведенные ранее соотношения (1.7) и (1.13), можно заменить R₁иR₂ эквивалентным сопротивлением R₁₂,а элементы R₃иR₄ –эквивалентным сопротивлением R₃₄:

R₃₄ = (1.19)

В результате такой эквивалентной замены получится схема, изображенная рис.1.3 (б), в которой элементы R₁₂ и R₃₄ соединены между собой последовательно. Для этой схемы эквивалентное сопротивление

В результате такой эквивалентной замены получим схему, изображенную на рис.1.3 (в). Определим ток, протекающий в этой цепи:

(1.21)

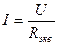
Это ток источника питания и ток в элементах R₁иR₂ реальной цепи. Найдем напряжения на участке цепи с сопротивлением R₁₂ и на участке цепи с сопротивлением R₃₄:

U₁₂ = I·R₁₂ ; U₃₄ = I ·R₃₄ (1.22)

Токи I₃ и I₄ можно найти по закону Ома:

(1.23)

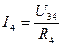
Для проверки правильности расчета схемы смешанного соединения элементов можно воспользоваться 1-м и 2-м законами Кирхгофа, а также законом баланса мощности. Должны выполняться соотношения:

Подобным образом можно рассчитать и другие, более сложные схемы электрических цепей со смешанным соединением элементов.

Существуют и другие схемы эквивалентных преобразований, так как не все схемы сводятся к комбинации последовательно и параллельно соединенных элементов. Такие схемы будут рассмотрены в следующем подразделе.

ЛЕКЦИЯ 2.

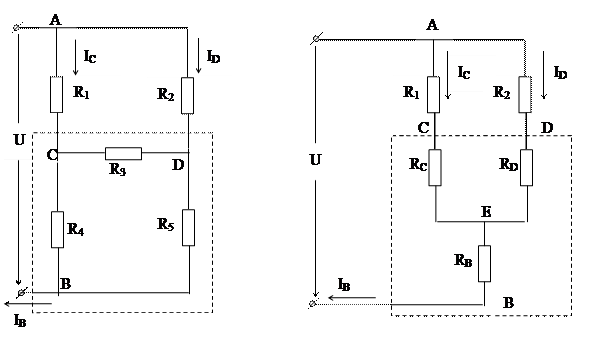
При эквивалентном преобразовании часть цепи заменяется новыми элементами с другим их соединением. При этом сопротивления новых элементов должны быть такими, чтобы проведенная замена не привела к изменению распределения токов и напряжений в участках цепи, не подвергшихся изменениям. В этом случае новую цепь можно считать эквивалентной старой.

Рассмотрим проводимость обеих схем между узлами В-С. В исходной схеме эта проводимость осуществляется по двум каналам протекания тока: через резистор R_A (его проводимость равна ) и через цепочку резисторов (её проводимость равна ).

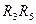
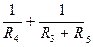
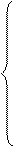
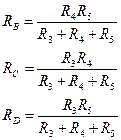
Суммарная проводимость обоих каналов составляет . В схеме замещения проводимость между этими же узлами осуществляется по цепочке резисторов R_B R_C и равна . Проводимости в обеих схемах должны быть равными.

=> (1.24)

Рассчитанная таким образом схема замещения по своим свойствам эквивалентна исходной схеме. Расчет эквивалентного сопротивления схемы замещения не представляет труда.

(1.25)

т.е. . (1.26)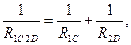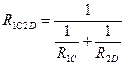

Теперь наша схема свелась к последовательному соединению элементов R_B и R_1C2D.

(1.27)

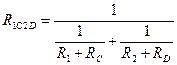
2. ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА.

Предварительные сведения. Параметры переменного тока.

В электрических цепях,электро-, радио- и других установках

широко применяются периодически изменяющиеся электродвижущие силы (э.д.с.), напряжения и токи. В электротехнике переменным токомпринято называть ток, изменяющий по закону:

Аналогично, переменным напряжением называют напряжение, изменяющееся по закону:

— циклическая частота,

f = (2.3)

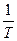
Здесь Т – период колебания.

В европейских странах в качестве стандарта частоты принята частота f = 50 Гц, в США и Японии стандарт частоты f = 60 Гц. Такие частоты обеспечивают получение оптимальных частот вращения электродвигателей переменного тока и отсутствие заметного для глаза мигания осветительных ламп накаливания. Следует отметить, что иногда бывает оправданным применение электротехнических устройств повышенной или пониженной частоты.

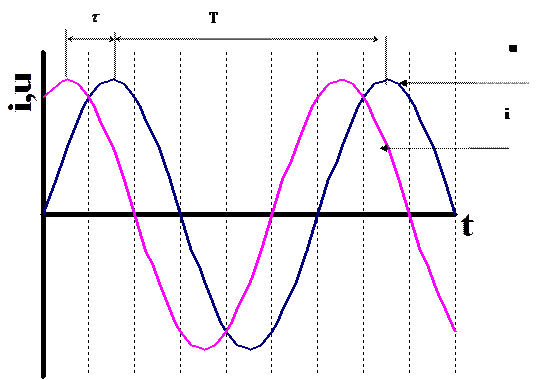
Графики переменного тока и переменного напряжения изображены на рис. 2.1.

Синусоидальный ток, так же как и постоянный, используется для совершения какой-либо работы, при этом электрическая энергия преобразуется в другие виды энергии (механическую, тепловую, и т.д.). Для того чтобы количественно оценить синусоидальный ток, используют значение постоянного тока, эквивалентного синусоидальному по совершаемой работе. Таким образом, вводится понятие действующего значения переменного тока.

Действующим значением переменного синусоидального токаназывается значение такого постоянного тока, при прохождении которого в одном и том же резисторе сопротивлением R за время одного периода Т выделяется столько же теплоты, сколько и при прохождении синусоидального тока.

При синусоидальном токе i = I_maxsinωt количество теплоты, выделяемое в резисторе R за время Т, согласно закону Джоуля-Ленца

= , (2.4)

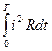
При постоянном токе количество теплоты, выделяемое за время Т

Согласно определению, Q

(2.6)

(2.7)

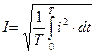
или: действующее значение синусоидального переменного тока

(2.8)

Аналогично, действующее значение синусоидального напряжения

(2.9)

Таким образом, действующие значения синусоидальных величин в 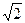раз меньше их амплитудных значений.

Электроизмерительные приборы всегда показывают действующие значения тока и напряжения. Зная их, всегда можно вычислить амплитудные значения. Так, например, если вольтметр показывает 220В синусоидального напряжения, то амплитуда такого напряжения равна 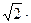220 = 311 В.

Источник

Смешанные электрические цепи

Смешанными называются электрические цепи, где имеют место различные вариации параллельного и последовательного соединений элементов. Эти цепи могут содержать различное число узлов, связей и разветвлений.

Смешанное соединение элементов

Смешанное соединение может содержать различные группы сопротивлений с последовательным и параллельным соединением.

Сопротивления \(R_3\) и \(R_cd\) соединены последовательно, при этом сопротивление участка ad рассчитается так:

Сложные электрические цепи со смешанным соединением элементов

Смешанное соединение очень часто можно встретить в электрических сетях. Оно представляет из себя комбинированные последовательные и параллельные соединения.

К примеру, если рассмотреть три элемента цепи, то два из них могут быть соединены параллельно, а третий подсоединен к ним последовательно.

При наличии большего числа приборов, смешанные цепи могут быть самыми разнообразными. Применяются даже более усложненные схемы, включающие более одного ЭДС-источника.

Не нашли что искали?

Просто напиши и мы поможем

Используют ряд методик для просчета таких цепей. Самой востребованной является методика, которая использует II закон Кирхгофа. Данный закон гласит о том, что алгебраическая сумма ЭДС замкнутого контура равняется алгебраической сумме падений напряжений.

Здесь учитывается именно алгебраическая сумма, без учета знаков, так как встречные ЭДС, так же как и напряжения, сформированные встречными токами, могут иметь разные знаки.

Встречается, что известны сопротивления отдельных участков и ЭДС сложных цепей. Для вычисления токов по II закону Кирхгофа, для замкнутых контуров формируют уравнения с неизвестными токами.

Также к данным уравнениям записываются уравнения точек разветвления, что составляются по I закону Кирхгофа. Решив такую систему уравнений, находят токи. Если цепи очень сложные, то данный метод будет очень громоздким, поскольку в уравнениях будет большое количество неизвестных.

Смешанное соединение резисторов

Резистор – это прибор, который имеет стабильную величину сопротивления. Это дает возможность регулировать остальные параметры цепи. Среди других видов соединений различают смешанное соединение резисторов.

От выбора типа соединения сопротивлений зависит устойчивость напряжения цепи и распределение по ней токов. Смешанное соединение являет собой набор соединений активных сопротивлений, выполненных последовательно и параллельно. Для расчета смешанных цепей, необходимо для начала рассматривать каждый узел отдельно.

Схемы смешанного типа характеризуются свойствами параллельных и последовательных соединений резисторов.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Сопротивление \(R_<1и2и3>\) соединенных параллельно резисторов, рассчитается так:

Смешанному соединению характерны как положительные, так и отрицательные характеристики. Данный тип соединения очень часто используют на практике в схемах электрических сетей.

Не нашли нужную информацию?

Закажите подходящий материал на нашем сервисе. Разместите задание – система его автоматически разошлет в течение 59 секунд. Выберите подходящего эксперта, и он избавит вас от хлопот с учёбой.

Гарантия низких цен

Все работы выполняются без посредников, поэтому цены вас приятно удивят.

Доработки и консультации включены в стоимость

В рамках задания они бесплатны и выполняются в оговоренные сроки.

Вернем деньги за невыполненное задание

Если эксперт не справился – гарантируем 100% возврат средств.

Тех.поддержка 7 дней в неделю

Наши менеджеры работают в выходные и праздники, чтобы оперативно отвечать на ваши вопросы.

Тысячи проверенных экспертов

Мы отбираем только надёжных исполнителей – профессионалов в своей области. Все они имеют высшее образование с оценками в дипломе «хорошо» и «отлично».

Гарантия возврата денег

Эксперт получил деньги, а работу не выполнил?
Только не у нас!

Деньги хранятся на вашем балансе во время работы над заданием и гарантийного срока

Гарантия возврата денег

В случае, если что-то пойдет не так, мы гарантируем возврат полной уплаченой суммы

Источник

Смешанное соединение и сложные электрические цепи

Такая цепь имеет два последовательно включенных участка, один из которых представляет собой параллельное соединение. По другой схеме соединены последовательно два прибора, а параллельно к ним подключен третий (рис. 1, б). Эту цепь следует рассматривать как параллельное соединение, в котором одна ветвь сама является последовательным соединением.

При большем количестве приборов могут быть различные, более сложные схемы смешанного соединения. Иногда встречаются более сложные цепи, содержащие несколько источников ЭДС.

Рис. 1. Смешанное соединение резисторов

Для расчета сложных цепей существуют различные методы. Наиболее общим из них является применение второго закона Кирхгофа. В самом общем виде этот закон гласит, что во всяком замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений.

Необходимо брать алгебраическую сумму потому, что ЭДС, действующие навстречу друг другу, или падения напряжения, созданные противоположно направленными токами, имеют разные знаки.

При расчете сложной цепи в большинстве случаев бывают известны сопротивления отдельных участков цепи и ЭДС, включенных источников. Чтобы найти токи, следует в соответствии со вторым законом Кирхгофа составить для замкнутых контуров уравнения, в которых токи являются неизвестными величинами. К этим уравнениям надо добавить уравнения для точек разветвления, составленные по первому закону Кирхгофа. Решая эту систему уравнений, определим токи. Конечно, для более сложных цепей этот метод получается довольно громоздким, так как приходится решать систему уравнений с большим числом неизвестных.

Применение второго закона Кирхгофа можно показать на следующих простейших примерах.

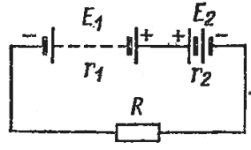
Пример 1. Дана электрическая цепь (рис. 2). ЭДС источников равны Е1= 10 В и Е2 = 4 В, а внутренние сопротивления г1 = 2 Ом и r2 = 1 Ом соответственно. ЭДС источников действуют навстречу. Нагрузочное сопротивление R = 12 Ом. Найти ток I в цепи.

Рис. 2. Электрическая цепь с двумя источниками, включенными навстречу друг другу

В левой его части имеем алгебраическую сумму ЭДС, а в правой части — сумму падений напряжений, создаваемых током I на всех последовательно включенных участках R, r1 и r 2.

Иначе уравнение можно написать в таком виде:

Подставив числовые значения, получим: I = (10 — 4) / (12 + 2 + 1 ) = 6/15 = 0,4 А.

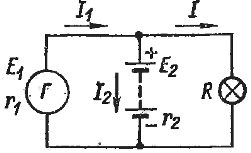
Пример 2. Более сложная схема представлена на рис. 3.

Рис. 3. Параллельная работа источников, имеющих разные ЭДС

Уравнение для контура, состоящего из генератора Е1 и лампочки, имеет вид Е1 = I1rl + I2r2.

Подставив в уравнения числовые значения величин и решив их совместно, получим: I1 = 5 А, I 2 = 1,5 А, I = 3,5 A, U = 10,5 В.

Напряжение на зажимах генератора на 1,5 В меньше его ЭДС, так как ток, равный 5 А, создает потери напряжения, равные 1,5 В, на внутреннем сопротивлении г1 = 0,3 Ом. Зато напряжение на зажимах аккумуляторной батареи больше ее ЭДС на 1,5 В, потому что батарея заряжается током, равным 1,5 А. Этот ток создает на внутреннем сопротивлении батареи (г2 = 1 Ом) падение напряжения, равное 1,5 В, оно и прибавляется к ЭДС.

Не следует думать, что напряжение U всегда будет средним арифметическим E 1 и Е2, как это оказалось в данном частном случае. Можно только утверждать, что в любом случае U должно находиться между Е1 и Е2.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

ElectronicsBlog

Обучающие статьи по электронике

Электротехника часть 4. Соединение элементов цепи

Всем доброго времени суток. В прошлой статье я рассмотрел закон Ома, применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса токов, называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и сопротивлениями.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Последовательное соединение приемников энергии

Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии

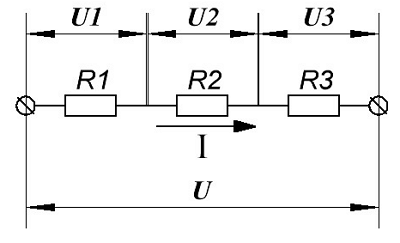
Пример последовательного подключения приемников энергии.

В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с напряжением U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления

Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.

Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями

где R – эквивалентное последовательное сопротивление.

Применение последовательного соединения

Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр

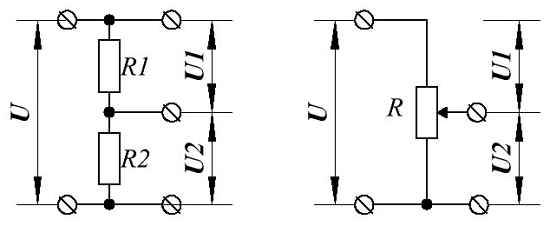
Делитель напряжения (слева) и потенциометр (справа).

В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.

Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.

Параллельное соединение приемников энергии

Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже

Пример параллельного соединения приемников энергии.

Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви

Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений

Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.

Смешанное соединение приемников энергии

Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии

Пример смешанного соединения приемников энергии.

В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид

В результате получили цепь из двух последовательных приемников энергии R₁₂R₃₄₅ эквивалентное сопротивление и ток, протекающий через них, составит

Тогда падение напряжения по участкам составит

Тогда токи, протекающие через каждый приемник энергии, составят

Первый закон Кирхгофа

Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.

Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением

где ∑ — обозначает алгебраическую сумму.

Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа

Изображение первого закона Кирхгофа.

На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид

Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.

Второй закон Кирхгофа

Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением

В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур

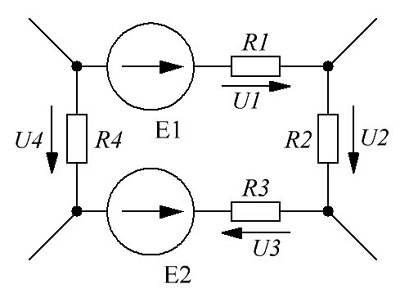
Схема, иллюстрирующая второй закон Кирхгофа.

Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид

Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Источник