Что такое сокращенное наименование в математике
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
СОКРАЩЁННЫЕ ОБОЗНАЧЕНИЯ ЕДИНИЦ ВЕЛИЧИН
а. е.- астрономическая единица
а. е. м.- атомная единица массы
О единицах, во. много раз больших или меньших, см. статьи Дольные единицы и Кратные единицы.
Смотреть что такое «СОКРАЩЁННЫЕ ОБОЗНАЧЕНИЯ ЕДИНИЦ ВЕЛИЧИН» в других словарях:
Сокращённые обозначения единиц величин — А ампер Ǻ ангстрем ат атмосфера техническая атм атмосфера физическая бар бар Бк беккерель Бэр биологический эквивалент рентгена В вольт В•А вольт ампер Вт ватт Вт•ч ватт час г грамм Г генри га гектар Гб гильберт Гс гаусс Гц герц… … Ветеринарный энциклопедический словарь
Международная система единиц — Запрос «СИ» перенаправляется сюда; см. также другие значения. Иное название этого понятия «SI»; см. также другие значения. Эту страницу предлагается переименовать в Система интернациональная. Пояснение прич … Википедия
СИ — У этого термина существуют и другие значения, см. СИ (значения). У слова «Си» есть и другие значения: см. Си. У слова «SI» есть и другие значения: см. SI. Даты перехода на метрическую систему … Википедия
САНТИ — САНТИ. первая составная часть наименований единиц физ. величин, служащая для обозначения единиц, равных Z доле исходных. Сокращённые обозначения с: 1 см (сантиметр) = 0,01 м … Большая политехническая энциклопедия
История арифметики — Арифметика. Роспись Пинтуриккьо. Апартаменты Борджиа. 1492 1495. Рим, Ватиканские дворцы … Википедия
Знаки валют — … Википедия
Планк, Макс — Эта статья о немецком физике. Другие значения термина в заглавии статьи см. на Планк (значения). Макс Планк Max Planck … Википедия
Двоичные приставки — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия
История математики — История науки … Википедия
Системы наименования чисел
Существуют две системы наименования чисел — американская и европейская (английская).
Содержание
Американская система
В некоторых странах, в том числе и в России, вместо слова «биллион» используется слово « миллиард ».
Европейская (английская) система
Европейская (английская) или длинная система наименования наиболее распространена в мире. Названия чисел в этой системе строятся так: к латинскому числительному добавляют суффикс «-иллион», название следующего числа (в 1 000 раз большего) образуется из того же самого латинского числительного, но с суффиксом «-иллиард». То есть после триллиона в этой системе идёт триллиард, а только затем квадриллион, за которым следует квадриллиард и т. д. Количество нулей в числе, записанном по европейской системе и оканчивающегося суффиксом «-иллион», определяется по формуле 6·x (где x — латинское числительное) и по формуле 6·x+3 для чисел, оканчивающихся на «-иллиард».
Возникновение и развитие
Обе системы возникли во Франции — Французский физик и математик Николя Шуке (Nicolas Chuquet) придумал слова «биллион» (byllion) и «триллион» (tryllion) и использовал их для обозначения чисел 10 12 и 10 18 соответственно, что послужило основой европейской системы.
Но некоторые французские математики в XVII веке использовали слова «биллион» и «триллион» для чисел 10 9 и 10 12 соответственно. Такая система именования укрепилась во Франции и в Америке и стала называться американской, а первоначальная система Шоке продолжала использоваться в Великобритании и Германии. Франция в 1948 году вернулась к системе Шоке (т. е. европейской).
Сравнение систем
Таблица от значения к названию
| Порядок | Значение | Название | СИ | |||
|---|---|---|---|---|---|---|
| Американская система | Логика построения | Европейская система | Логика построения | |||
| 0 | 10 0 | один | один | |||
| 1 | 10 3 | тысяча | 1 000 1 + 0 | тысяча | 1 000 000 0,5 | кило |
| 2 | 10 6 | миллион | 1 000 1 + 1 | миллион | 1 000 000 1,0 | мега |
| 3 | 10 9 | биллион | 1 000 1 + 2 | тысяча миллионов ( миллиард ) | 1 000 000 1,5 | гига |
| 4 | 10 12 | триллион | 1 000 1 + 3 | биллион | 1 000 000 2,0 | тера |
| 5 | 10 15 | квадриллион | 1 000 1 + 4 | тысяча биллионов ( биллиард ) | 1 000 000 2,5 | пета |
| 6 | 10 18 | квинтиллион | 1 000 1 + 5 | триллион | 1 000 000 3,0 | экса |
| 7 | 10 21 | секстиллион | 1 000 1 + 6 | тысяча триллионов ( триллиард ) | 1 000 000 3,5 | зетта |
| 8 | 10 24 | септиллион | 1 000 1 + 7 | квадриллион | 1 000 000 4,0 | йотта |
Таблица от названия к значению
См. также
Ссылки
la:Scalae longae et breves nl:Korte en lange schaalverdeling
Сокращенное умножение: правила, формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
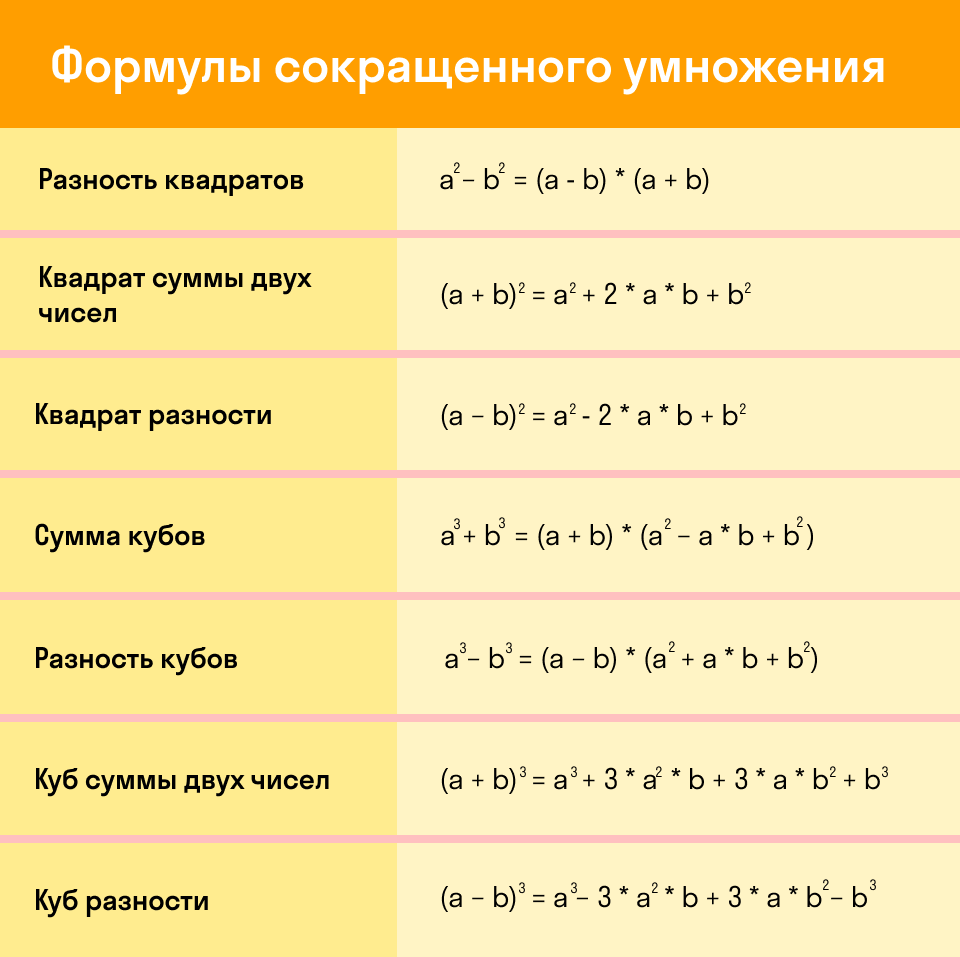
Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.
Доказательство формул сокращенного умножения
Остальные ФСУ можно доказать аналогичным методом.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).
Для четных показателей можно записать так:
a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).
Для нечетных показателей:
a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с 3 – 8.
Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).
Задание 3
Как решаем:
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ И АББРЕВИАТУР
арт.- артиллерийский, артист
ат. м.- атомная масса
ат. н.- атомный номер
б. ч.- большая часть, большей частью
в. д.- восточная долгота
верх.- верхний, верховный
вкл.- включая, включительно
вод.- водный, водяной
гл. обр.- главным образом
з. д.- западная долгота
изд.- издание, издатель
ин. ч.- иностранный член
инж.- инженер, инженерный
иссл.- исследование, исследовал
к.-л.- какой-либо, кто-либо
косм. кор.- космический корабль
лаб.- лаборатория, лабораторный
мн. ч.- множественное число
мол. м.- молекулярная масса
наз.- называемый, называется
назв.- название, назван
наиб.- наиболее, наибольший
наим.- наименее, наименьший
нач.- начало, начальник, начальный
неизв.- неизвестно, неизвестный
обл.- область, областной
окр.- округ, окружной
осн.- основан(ный), основной
отд.- отдел, отдельный
первонач.- первоначально, первоначальный
ред.- редактор, редакция
рт. ст.- ртутный столб
с. ш.- северная широта
сер.- середина, серия
собств.- собственно, собственный
совм.- совместно, совместный
созд.- создал, создан(ный)
сокр.- сокращение, сокращённо
соотв.- соответственно, соответствующий
ст.- станция, статья, старший
ст. ст.- старый стиль
т. н.- так называемый
т. экз.- тысяч экземпляров
тв.- твёрдость, твёрдый
терр.- территория, территориальный
тыс.- тысяча, тысячелетие
устар.- устаревший, устарелый
цитол.- цитологический
ч.- часть, человек
Примечания. 1. В Словаре применяются сокращения слов, обозначающих государственную, языковую или национальную принадлежность
(напр., англ.- английский, рус.- русский), название месяцев (напр., апр.- апрель, апрельский). 2. В прилагательных и причастиях допускается
отсечение окончаний и суффиксов: «альный», «анный», «ельный», «ельский», «енный», «еский», «иальный», «ионный», «ованный» и др. (напр.,
центр., иностр., значит., издат., естеств., арктич., колон., дистанц., механизир.). 3. Аббревиатуры, встречающиеся в тексте статей, но не вошедшие
в этот список, следует искать непосредственной Словаре.
Полезное
Смотреть что такое «СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ И АББРЕВИАТУР» в других словарях:
Список аббревиатур — Это служебный список статей, созданный для координации работ по развитию темы. Данное предупреждение не устанавливается на информационные списки и глоссарии … Википедия
Имена советского происхождения — Имена советского происхождения личные имена, бытующие в языках народов бывшего СССР, например в русском,[1][2] татарском[3] и украинском … Википедия
Стилистика (лингвистика) — У этого термина существуют и другие значения, см. Стилистика (значения). Лингвистика … Википедия