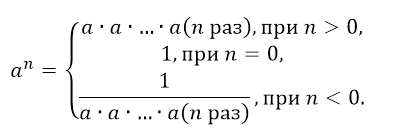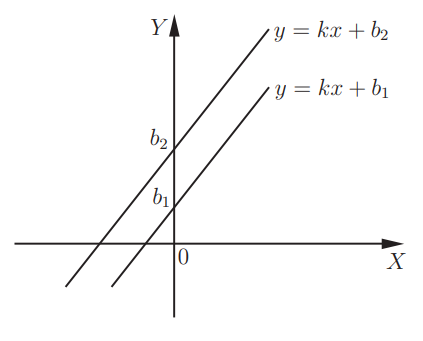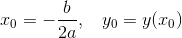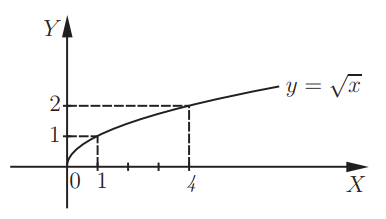Что такое степенная функция определение

Функция. Степенная функция.

Так как нулевая степень всякого числа, не равного нулю, равна единице, то при n = 0 степенная функция становится постоянной величиной, т.е. у = а. Поясним подробнее: выражение ноль в нулевой степени неопределенно, в том случае, когда функция у = ax 0 для всех значений х, естественно кроме нуля, равна а, и следовательно, если х = 0, то у = а. В таком случае график представлен прямой линией, параллельной оси абсцисс).

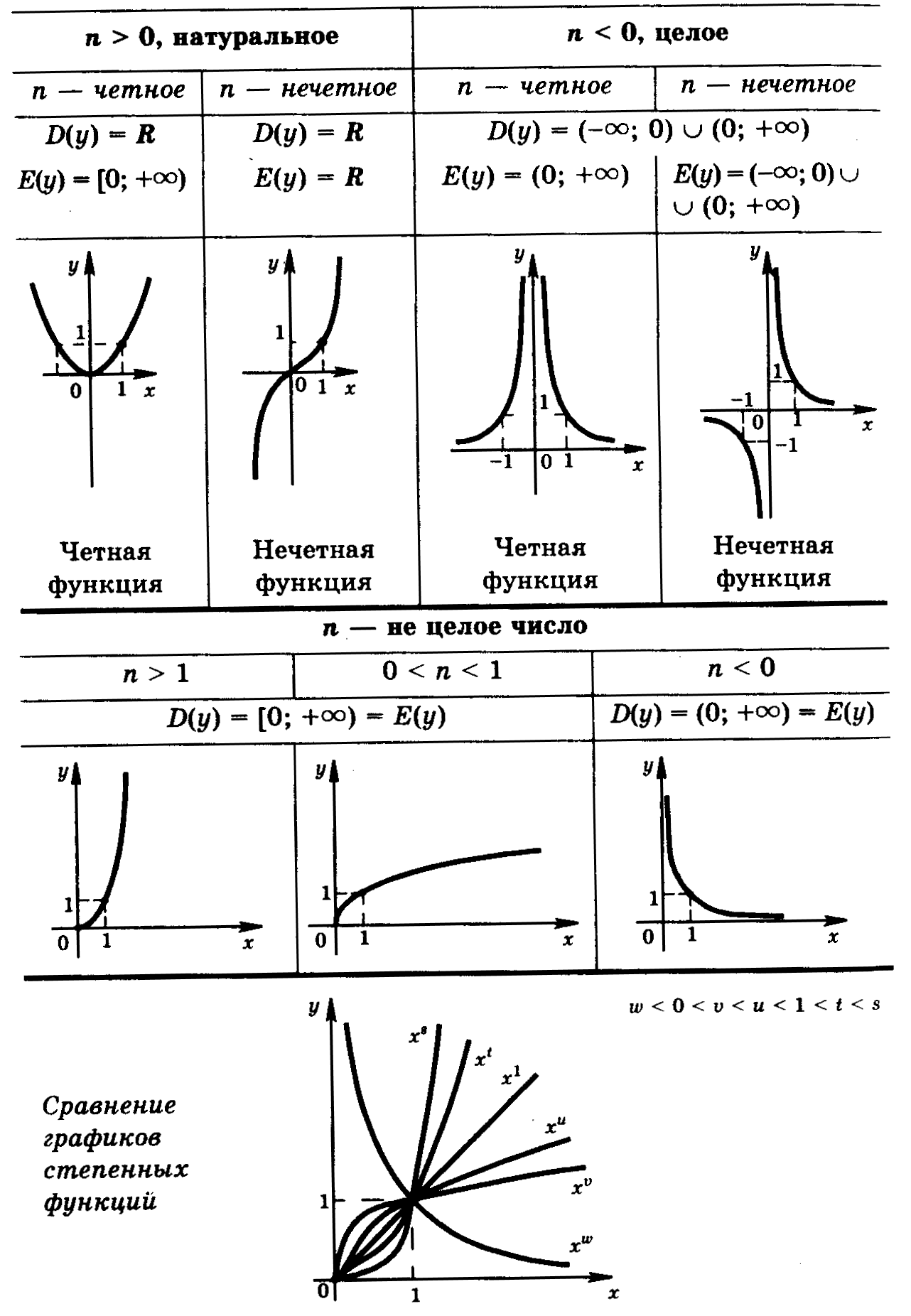
Остальные случаи делятся на группы:

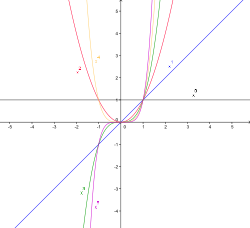
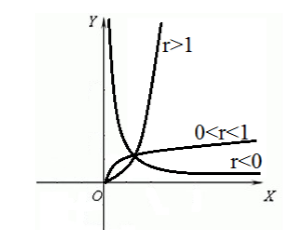
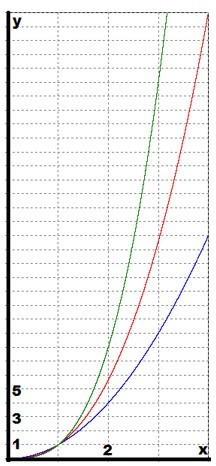
Видны графики функции у = х n при n = 0,1; 1/4; 1/3; 1/2; 2/3; 1;3/2; 2 ; 3; 4; 10. Все они проходят через начало координат и точку (1; 1).

При n = 1 получаем прямую являющуюся биссектрисой угла х0у.

При n > 1 график образуется сначала между х = 0 и х = 1, несколько ниже этой прямой, а затем при х > 1, выше ее.

По аналогии с графиком функции у = ах 2 графики всех степенных функций у = ах n при положительном n называют параболами n-го порядка или n-й степени. Так, график функции у = ах 3 называется параболой 3-го порядка или кубической параболой.

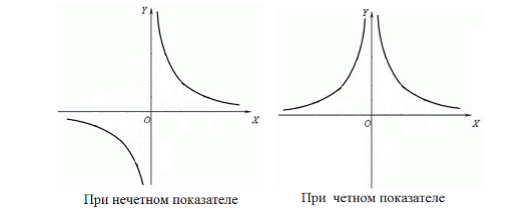
В случае если n дробное число p/q с четным знаменателем q и нечетным числителем р, то величина может иметь два знака , а у графика появляется еще одна часть внизу оси абсцисс х, причем она симметрична верхней части.

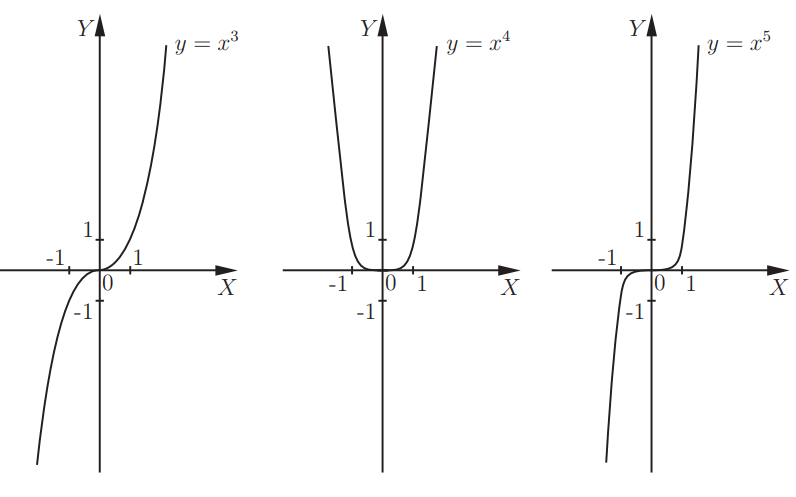
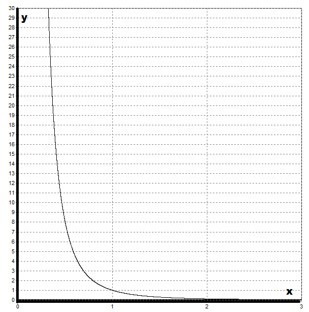
Все графики неограниченно приближаются как к оси абсцисс х, так и к оси ординат у, не соприкасаясь с ними. Вследствие сходства с гиперболой эти графики называют гиперболами n -го порядка.

Источник

Степенная функция

Содержание

Вещественная функция

Область определения

Если показатель степени — целое число, то можно рассматривать степенную функцию на всей числовой прямой (кроме, возможно, нуля). В общем случае степенная функция определена при 0″ border=»0″ />. Если 0″ border=»0″ />, то функция определена также и при , иначе нуль является её особой точкой.

Рациональный показатель степени

Пример: из третьего закона Кеплера вытекает, что период T обращения планеты вокруг Солнца связан с большой полуосью A её орбиты соотношением: (полукубическая парабола).

Свойства

Комплексная функция

Степенная функция комплексного переменного z, вообще говоря, определяется формулой [3] :

Здесь показатель степени c — некоторое комплексное число. Значение функции, соответствующее главному значению логарифма, называется главным значением степени. Например, значение равно где k — произвольное целое, а его главное значение есть

Комплексная степенная функция обладает значительными отличиями от своего вещественного аналога. В силу многозначности комплексного логарифма она, вообще говоря, также имеет бесконечно много значений. Однако два практически важных случая рассматриваются отдельно.

См. также

Литература

Ссылки

Примечания

Полезное

Смотреть что такое «Степенная функция» в других словарях:

Степенная функция — функция f (x) = ха, где а фиксированное число (см. Степень). При действительных значениях основания х и показателя а обычно рассматривают лишь действительные значения С. ф. xa. Они существуют, во всяком случае, для всех х > 0; если а… … Большая советская энциклопедия

СТЕПЕННАЯ ФУНКЦИЯ — функция вида y = axn, где a и n любые действительные числа … Большой Энциклопедический словарь

СТЕПЕННАЯ ФУНКЦИЯ — ф ция вида у = ахn, где а и п действит. числа, С. ф. охватывает большое число закономерностей в природе. На рис. изображены графики С. ф. для п = 1, 2, 3, 1/2 и а = 1. К ст. Степенная функция … Большой энциклопедический политехнический словарь

степенная функция — функция вида у=axn, где а и n любые действительные числа. На рисунке изображены графики степенной функции для n = 1, 2, 3, 1/2 и а = 1. * * * СТЕПЕННАЯ ФУНКЦИЯ СТЕПЕННАЯ ФУНКЦИЯ, функция вида y = axn, где a и n любые действительные числа … Энциклопедический словарь

степенная функция — laipsninė funkcija statusas T sritis automatika atitikmenys: angl. power function vok. Potenzfunktion, f rus. степенная функция, f pranc. fonction puissance, f … Automatikos terminų žodynas

СТЕПЕННАЯ ФУНКЦИЯ — функция вида у = ахn, где а и п любые действительные числа. На рис. изображены графики С. ф. для n= 1, 2, 3, 1/2 и a=1 … Естествознание. Энциклопедический словарь

функция спроса — Функция, которая показывает, как меняется объем продаж конкретного продукта в зависимости от его цены при равных маркетинговых усилиях по его продвижению на рынок. [http://www.lexikon.ru/dict/fin/a.html] функция спроса Функция, отражающая… … Справочник технического переводчика

Функция спроса — [demand function] функция, отражающая зависимость объема спроса на отдельные товары и услуги (потребительские блага) от комплекса факторов, влияющих на него. Более узкая трактовка: Ф.с.выражает взаимозависимость между спросом на товар и ценой… … Экономико-математический словарь

Источник

Степенная функция

Расскажем подробно об этих функциях и их графиках.

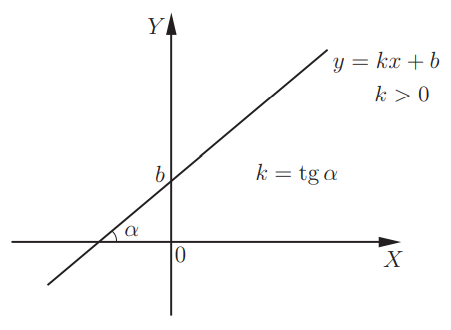
1. Линейная функция y = kx + b. График — прямая линия. Для её построения достаточно двух точек.

Если k > 0, линейная функция возрастает. Чем больше k, тем круче идет график. Число k называется угловым коэффициентом прямой и равно тангенсу угла наклона этой прямой к положительному направлению оси X:

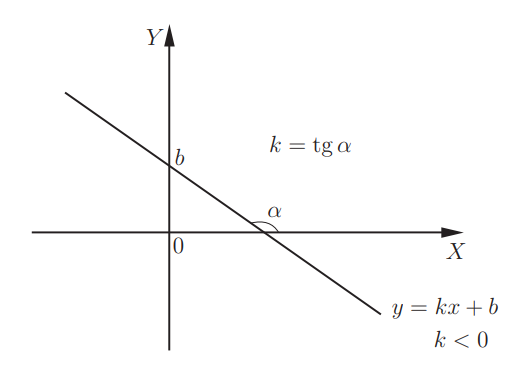
Если k 2 + bx + c мы уже рассказывали.

Кратко повторим основные моменты:

— Если a > 0, ветви параболы направлены вверх. Если a 2 + bx + c = 0. Если корней нет (дискриминант уравнения меньше нуля), парабола не пересекает ось X.

— Точку пересечения параболы с осью Y находим, подставив в её уравнение x = 0.

4. Заметим, что между функциями y = x 2 и y = x 4 есть определенное сходство. Оба этих графика симметричны относительно оси Y. Такие функции называются чётными.

Определение. Функция y = f(x) называется чётной, если:
1) область определения функции симметрична относительно нуля;
2) для каждого x из области определения выполняется равенство f(−x) = f(x).

Графики функций y = x 3 и y = x 5 симметричны относительно начала координат. Эти функции — нечётные.

Очевидно, функция y = x α является чётной при чётных значениях α и нечётной при нечётных α.

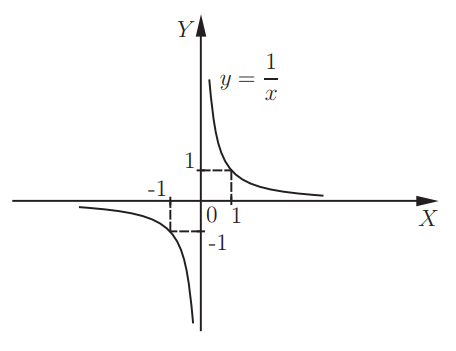
Выражение определено при x ≥ 0, поэтому область определения функции — все неотрицательные числа.

Кроме того, принимает только неотрицательные значения, поскольку ≥ 0.

Мы используем эти свойства при решении уравнений и неравенств. Уравнение вида имеет смысл только при f(x) ≥ 0 и g(x) ≥ 0. Это его область допустимых значений.

Правильный ответ:

Запомните это. Проверить легко: возьмём, например, a = −2.

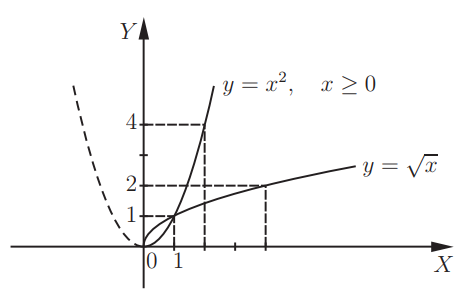
Сейчас нас интересует правая ветвь параболы, при x ≥ 0. Мы видим, что эта часть параболы и график функции словно нарисованы по одному шаблону, по-разному расположенному в координатной плоскости. Они симметричны относительно прямой y = x. То, что для одной из них — область определения, для другой — область значений.

Напомним, что такие функции называются взаимно-обратными. Подробно об этом можно прочитать в статье «Логарифмическая функция»).

7. Легко убедиться, что функция является обратной к функции y = x 3

Источник

Степенная функция

Вы будете перенаправлены на Автор24

Для удобства рассмотрения степенной функции будем рассматривать 4 отдельных случая: степенная функция с натуральным показателем, степенная функция с целым показателем, степенная функция с рациональным показателем и степенная функция с иррациональным показателем.

Степенная функция с натуральным показателем

Для начала введем понятие степени с натуральным показателем.

Рассмотрим теперь степенную функцию с натуральным показателем, её свойства и график.

$f\left(x\right)=x^n$ ($n\in N)$ называется степенной функцией с натуральным показателем.

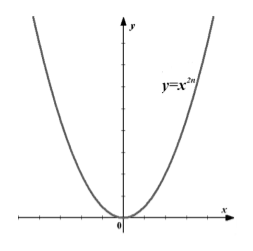
Свойства степенной функции с натуральным четным показателем

$f(x)\ge 0$ на всей области определения

Функция выпукла на всей области определения.

Поведение на концах области определения:

Готовые работы на аналогичную тему

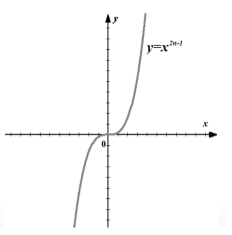
Свойства степенной функции с натуральным нечетным показателем

Функция возрастает на всей области определения.

\[2\left(2n-1\right)\left(n-1\right)\cdot x^<2n-3>=0\] \[x=0\]

Степенная функция с целым показателем

Для начала введем понятие степени с целым показателем.

Рассмотрим теперь степенную функцию с целым показателем, её свойства и график.

$f\left(x\right)=x^n$ ($n\in Z)$ называется степенной функцией с целым показателем.

Свойства степенной функции с отрицательным целым показателем

Если показатель четный, то функция четна, если нечетный, то функция нечетна.

$f(x)\ge 0$ на всей области определения

Степенная функция с рациональным и иррациональным показателем

$f\left(x\right)=x^r$ ($r\in Q)$ называется степенной функцией с рациональным показателем.

$f\left(x\right)=x^r$ ($r\in J)$ называется степенной функцией с иррациональным показателем.

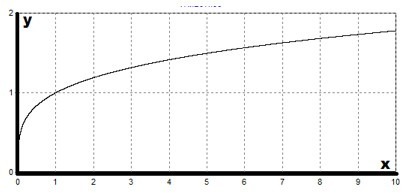
Приведем графики степенных функций с рациональным и иррациональным показателем (рис. 5). Рассмотреть, аналогично, свойства этих функции оставим читателю.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 03 2021

Источник

Свойства степенных функций, построение графиков

Степенная функция — что это такое

К степенным функциям в теории относятся следующие виды:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Исходя из обозначения, при x≥0, область определения рассматриваемой функции – это луч [0;+∞).

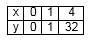
Далее следует записать таблицу значений:

Затем можно сравнить несколько степенных функции следующим способом:

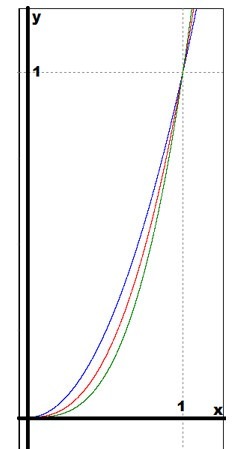
Число 2,5 находится между 2 и 3. В таком случае можно предположить, что и график рассматриваемой функции расположен между соответствующими графиками. Можно представить разные характеристики х, чтобы сравнить значения функций, которые зависят от x:

Все графики целесообразно построить на одном рисунке. В первом случае \(0 :

Линейная функция y = kx + b. Графиком данной функции является прямая линия. Для того, чтобы ее построить, требуется пара точек. При k > 0, линейная функция будет расти. При увеличении k график становится круче. Значение k представляет собой угловой коэффициент прямой и равно тангенсу угла наклона рассматриваемой прямой к положительному направлению оси X:

При использовании k

При k = 0, на графике будет изображена прямая y = b, которая параллельна оси X. В том случае, когда имеет место равенство угловых коэффициентов прямых, прямые будут параллельны друг другу.

Квадратичная функция \(y = ax2 + bx + c\) представляет собой параболу. Она обладает рядом особенностей:

Функция \(y = x^<3>\) является кубической параболой. Можно представить ее на рисунке, а также функции \( y = x^<4>\) и \(y = x^<5>.\)

Можно отметить, что функции \(y = x^<2>\) и \(y = x^<4>\) обладают некоторыми сходствами. Графики являются симметричными по отношению к оси Y. В данном случае можно сказать, что рассматриваемые функции – четные.

Функция \(y = f(x)\) является четной, когда:

Графики функций \(y = x^<3>\) и \(y = x^<5>\) симметричны по отношению к началу координат. Данные функции являются нечетными.

Функция \(y = f(x)\) – нечетная, при условии, что:

То, что для одной из них является областью определения, для другой — представляет собой область значений. Данные функции носят название взаимно-обратных.

Виды и их свойства, область определения

Степенные функции обладают рядом специфических свойств, которые могут отличаться в зависимости от их вида. Рассмотрим основные из них.

График имеет следующий вид:

В том случае, когда x>0, а r – какое-либо рациональное число, производная степенной функции \(y=x^r\) определяется, согласно формуле:

Степенная функция с рациональным и иррациональным показателем

Степень действительного числа a, обладающего рациональным показателем n вычисляется, согласно уравнению:

Функция \( f(x)=x^(r\in Q)\) представляет собой степенную функцию с рациональным показателем.

Функция \(f(x)=x^(r\in J)\) представляет собой степенную функцию с иррациональным показателем.

Как строить графики степенных функций

График функции является множеством точек, у которых абсциссы являются допустимыми значениями аргумента х, а ординаты – соответствующими значениями функции y.

Согласно определению, построить график какой-либо функции можно путем поиска всех пар соответствующих значений аргумента и функции. Как правило, в результате получается бесконечное множество точек, что затрудняет процесс построения графика. В связи с этим требуется исследовать функцию:

Задачи со степенной функцией

Необходимо определить максимальное и минимальное значения для функции \(y=x^<\frac<5><2>>\) на отрезке:

Показатель степени рассматриваемой функции обладает положительным значением. В этом случае, учитывая свойства записанной функции, можно заключить, что она возрастает на всей области определения. Таким образом, функция достигает своего максимума и минимума на концах заданных отрезков (если она определена в этих точках).

На промежутке (2,10) максимальное и минимальное значения функции отсутствуют, в связи с тем, что промежуток является открытым, и точки 0 и 4 к данному интервалу не относятся.

На луче [9;+∞) наибольшее значение отсутствует

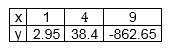
Требуется определить максимальное и минимальное значение на отрезке [1;9] для функции:

Вычислим производную рассматриваемой функции:

Так как производная существует на всей области определения исходной функции, можно заключить, что критические точки отсутствуют.

Далее определим стационарные точки:

Заданному отрезку принадлежит только одно решение \(x_2=4\)

Построим таблицу значений нашей функции на концах отрезка и в точке экстремума:

График функции \(y=x^<\frac<4><3>>\) будет возрастать, а график функции \(у=24-х\) – убывать. Известно, что когда одна функция возрастает, а вторая убывает, то будет лишь одна точка, в которой эти функции пересекаются. Следовательно, уравнение обладает всего одним решением. Можно заметить, что:

Таким образом, при х=8 уравнение преобразуется в справедливое равенство: 16=16, что является ответом к задаче.

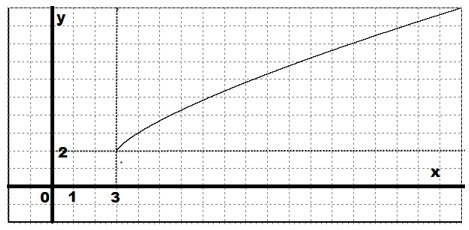
Необходимо построить график функции с объяснениями: \(y=(x-3)^\frac<3><4>+2\)

График рассматриваемой функции можно получить из графика функции:

Требуется сместить этот график на 3 единицы в правую сторону и на 2 единицы вверх:

Требуется записать уравнение для касательной к прямой \(y=x^<-\frac<4><5>>\) в точке х=1.

Обозначение уравнения касательной:

По условию задачи число a является натуральным числом 1, поэтому:

Источник