Что такое обучающая выборка назовите ее особенности
Выборка
Материал из MachineLearning.
Содержание
Выборка (sample, set) — конечный набор прецедентов (объектов, случаев, событий, испытуемых, образцов, и т.п.), некоторым способом выбранных из множества всех возможных прецедентов, называемого генеральной совокупностью.
Если исследователь не имеет возможности управлять выбором прецедентов, то обычно предполагается, что выбор прецедентов случаен. Если же выбором прецедентов можно управлять, то возникают задачи оптимального формирования выборки, см. также активное обучение, планирование экспериментов, выборочное обследование.
По каждому прецеденту собираются (измеряются) некоторые данные (data), образующие описание прецедента. Совокупность описаний всех прецедентов выборки является входной информацией для статистического анализа данных, интеллектуального анализа данных, машинного обучения.
Термины выборка (sample, set) и данные (data) взаимозаменяемы; иногда они употребляются вместе как один термин выборка данных (data set). Поэтому анализ данных можно понимать также как анализ конечных выборок. Основные цели анализа данных:
Вероятностная модель порождения данных
Случайная выборка
Вероятностная модель порождения данных предполагает, что выборка из генеральной совокупности формируется случайным образом. Объём (длина) выборки считается произвольной, но фиксированной, неслучайной величиной.
Однородная выборка
Независимая выборка
Простая выборка
Простая выборка — это случайная, однородная, независимая выборка (i.i.d. — independent, identically distributed).
Эквивалентное определение: выборка простая, если значения являются реализациями независимых одинаково распределённых случайных величин.
Простая выборка является математической моделью серии независимых опытов. На гипотезу простой выборки существенно опираются многие методы статистического анализа данных и машинного обучения, в частности, большинство статистических тестов, а также оценки обобщающей способности в теории вычислительного обучения.
Также существует множество методов, не предполагающих однородность и/или независимость выборки, в частности, в теории случайных процессов, в прогнозировании временных рядов. Метод максимума правдоподобия позволяет оценивать значения параметров модели по обучающей выборке, в общем случае не требуя, чтобы выборка была однородной и независимой. Однако в случае простых выборок применение метода существенно упрощается.
Обучающая и тестовая выборка
Обучающая выборка (training sample) — выборка, по которой производится настройка (оптимизация параметров) модели зависимости.
Тестовая (или контрольная) выборка (test sample) — выборка, по которой оценивается качество построенной модели. Если обучающая и тестовая выборки независимы, то оценка, сделанная по тестовой выборке, является несмещённой.
Оценку качества, сделанную по тестовой выборке, можно применить для выбора наилучшей модели. Однако тогда она снова окажется оптимистически смещённой. Для получения немсещённой оценки выбранной модели приходится выделять третью выборку.
Проверочная выборка (validation sample) — выборка, по которой осуществляется выбор наилучшей модели из множества моделей, построенных по обучающей выборке.
Что такое обучающая выборка назовите ее особенности
Искусственные нейронные сети (ИНС) в последнее время стали широко популярны как метод обработки данных. Они представляют собой математические модели биологических нейронов, способные изменять свою структуру под воздействием внешних факторов. В ходе обучения внутренние параметры искусственной нейронной сети подстраиваются под входные данные, что позволяет выделять в них закономерности или решать задачи прогнозирования, классификации и кластеризации [1].
В практическом здравоохранении, где не всегда имеется возможность располагать полным набором входных данных, особый интерес представляют экспертные системы для диагностики заболеваний на основе нейронных сетей [2]. Искусственные нейронные сети сегодня широко применяются в выявлении атеросклеротических бляшек с помощью анализа флюоресцентных спектров, диагностике инфаркта миокарда, заболеваний периферических сосудов, клапанных шумов сердца с помощью анализа акустических сигналов, распознавании психических симптомов и многих других направлениях медицины.
Применение нейронных сетей в процессе принятия решений сводится к следующему ряду особенностей:
Кроме того, нейронные сети позволяют принимать решения в условиях неопределенности путем решения задач с неизвестными закономерностями и зависимостями между входными и выходными данными, что позволяет работать с неполными данными [3]. Это означает, что нейронные сети способны создавать механизмы воспоминаний, которые могут обрабатывать неполные либо нечеткие входные данные и возвращать результат. Результатом могут быть сами входные данные или совершенно отличающиеся от входных данных ответы.
При решении задач машинного обучения принципиально важное значение имеют размер и качество обучающей выборки. В связи с этим формирование такой обучающей выборки является одной из первостепенных задач машинного обучения. Недостаточно точный тренировочный набор в большинстве случаев приводит к неверному формированию модели принятия решений и, как следствие, снижает эффективность самих алгоритмов обучения. Большинство специалистов по машинному обучению отмечают, что наличие хороших обучающих данных намного важнее качества алгоритма обучения.
В связи с активным развитием глубоких нейронных сетей в последнее десятилетие, вопросы формирования множества обучающих данных принимают особенно важное значение, поскольку во многих задачах глубокие нейронные сети демонстрируют качество, существенно превосходящее остальные алгоритмы машинного обучения. Однако, чтобы получить подобный выигрыш в качестве, необходимо использовать обучающее множество очень большого размера, а также специальные методы расширения и имитации расширения обучающего множества [4, 5].
Нейронные сети, в отличие от статистических методов многомерного классификационного анализа, базируются на параллельной обработке информации и обладают способностью к самообучению, то есть получать обоснованный результат на основании данных, которые не встречались в процессе обучения. Эти свойства позволяют нейронным сетям решать сложные (масштабные) задачи, которые на сегодняшний день считаются трудноразрешимыми [2, с. 6–8].
Изучение особенностей формирования обучающей выборки и обучения нейронной сети с неполными входными данными при решении частных медицинских задач
Материалы и методы исследования
В данной работе в качестве обучающей выборки применялись данные о состоянии здоровья 457 пациентов по 56 критериям на основе результатов эхокардиографического исследования. Так как в некоторых случаях наблюдалась неполнота входных данных для обучающей выборки, имеющийся набор тренировочных данных был поделен на категории по значимости:
Результатом работы нейронной сети являлось наличие одного или нескольких синдромов сердечно-сосудистых заболеваний:
Этапы нейросетевого анализа включали:
1. Исследование взаимосвязи переменных и понижение размерности.
2. Построение и обучение сетей разных типов.
3. Сравнение качества сетей и их статистических характеристик.
Понижение размерности предполагало отсев ряда входных, выбивающихся из общей закономерности параметров за счет осуществления корреляционного анализа и определения степени взаимозависимости входных параметров от выходных следующим образом:
Далее для каждого синдрома и соответствующего ему набора параметров построены различные модели нейронной сети со следующей структурой:
где N – количество входных нейронов для различных синдромов.
В качестве функций активации нейронов выбиралась либо гиперболическая тангенциальная функция активации, либо логистическая сигмоидальная функция активации, либо сочетание данных двух функций. Выбор данных функций обусловлен тем, что они могут быть настроены на получение на выходе результата между 0 и 1, где 0 – отсутствие синдрома заболевания, 1 – наличие синдрома. Промежуточные значения говорят о неоднозначности выявления данного синдрома в связи с неполнотой либо неоднозначностью исследования.
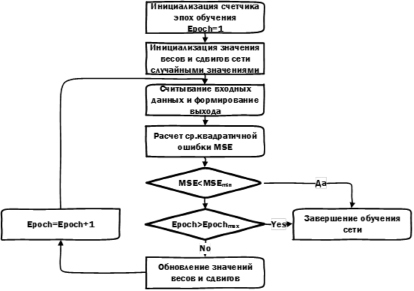
Всё обучение нейронной сети сводится к корректировке значений весов (синапсов) и отклонений (корректирующих сдвигов) значений нейронов сети путем применения алгоритма обратного распространения ошибки (рис. 1).
Обучаемость сети характеризуется числом допустимых циклов (эпох обучения) и допустимой среднеквадратичной ошибкой в расчете результата, достижение предельных значений которых завершает процесс обучения модели.
Проверка работоспособности построенной сети осуществлялась на тестовом наборе из 10 исследований, включавших помимо стандартных входных значений также и исследования, выбивающиеся из типичных показателей (таблица).
Как видно из результата, только одна нейронная модель смогла практически безошибочно выявить все синдромы заболеваний, выдавая ответы, подобные ответам эксперта (рис. 2). Также эксперимент показал, что нейронные сети, имеющие на выходном слое логистическую сигмоидальную функцию активации, ни разу не смогли опровергнуть наличие синдрома заболевания в отличие от гиперболической тангенциальной функции активации. Следовательно, данная функция активации для выходного слоя в данном круге задач неприменима.
Рис. 1. Обучение нейронной сети
Сравнительный анализ работы нейронных сетей различной структуры и ответов эксперта
Чувствительность методов ML к размеру обучающей выборки. Part 6.
В прошлом тексте я пробовал «помочь», нейросете уменьшив число рандомных фичей. Сейчас попробую помочь увеличив число примеров. Может наша сверточная сеть покажет что то вменяемое если увеличить число примеров до миллиона? Это задача на моем компьютере требует совершенно других затрат времени, так что я вчера запустил машинку обучаться, а сам пошел спать. Обучался на 50 эпохах, увеличивая данные от 10 тысяч до 50 тысяч (увеличивая обьем на 10 тысяч), и от 100 тысяч до 900 тысяч (с шагом +100 тысяч).
Результаты порадовали. Я не буду в 5 раз пересказывать логику «исследования», но убрав week=5 мы должны (ну как должны!? вообще то нам никто ничего не должен) получить равновероятный прогноз события 1 и события 0. Ниже на графике эту норму в 50% изображает серая линия. Красная это прогноз события=1, синяя событие=0, ось Х число примеров на обучающей выборке в тысячах.
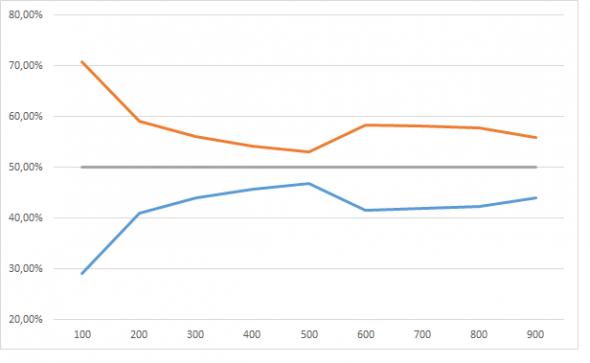
И пусть девочка кинет в меня камне если тут нет сходимости.
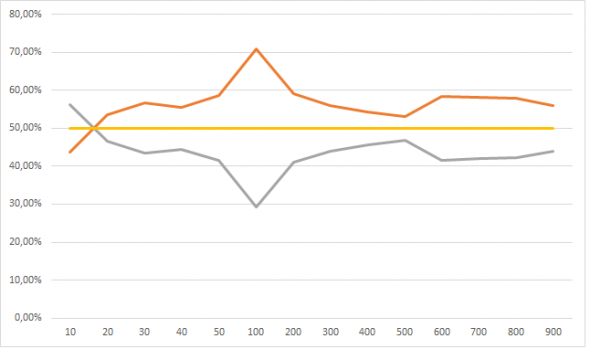
Но это динамика при увеличении обучающей выборки от 100 тысяч до 900 тысяч, а вот если сюда присовокупить от 10 тысяч до 50, тут все не так очевидно:
У меня следующее обьяснение: нейросеть большая фантазерка, в том смысле что способна найти в числах даже то чего там и нет. Но с другой стороны нельзя сложить из букв «п», «ж», «о», «а» слово вечность, поэтому когда обучающая выборка очень маленькая фантазии нейросети ограниченны. По мере роста обучающей выборки, нейросеть начинает находить все больше и больше черных кошек в черной комнате, которых там нет, и так до размера выборки в 100 тысяч примеров. По мере дальнейшего размера выборки фантазию нейросети начинает ограничивать реальность-сложно аппроксимировать 101 фичей данные размером в сотни тысяч. Ну это ИМХО.
Поставив week = 5 мы должны получить другой тип сходимости. Пробую обьяснить-если нейросеть правильно все разобрала, а именно поняла что единственная значимая фиxа это week и именно при week = 5, то число событий 1 она должна как можно чаще закидывать в week = 5. Смотрим:
Для GB я тоже потестил при обучении от 100 до 900 тысяч примеров и сравнил с нейросеткой:
| GB | Нейросеть | |||
| 0 | 1 | 1 | 0 | |
| 100 | ||||
| 1 | 53,75% | 46,25% | 43,43% | 56,57% |
| 2 | 53,76% | 46,24% | 64,38% | 35,62% |
| 3 | 53,54% | 46,46% | 82,30% | 17,70% |
| 4 | 54,05% | 45,95% | 92,54% | 7,46% |
| 5 | 0,79% | 99,21% | 97,20% | 2,80% |
| 200 | ||||
| 1 | 49,93% | 50,07% | 36,74% | 63,26% |
| 2 | 52,58% | 47,42% | 52,03% | 47,97% |
| 3 | 54,95% | 45,05% | 66,08% | 33,92% |
| 4 | 55,23% | 44,77% | 81,28% | 18,72% |
| 5 | 0,09% | 99,91% | 98,82% | 1,18% |
| 300 | ||||
| 1 | 46,79% | 53,21% | 40,75% | 59,25% |
| 2 | 47,83% | 52,17% | 50,54% | 49,46% |
| 3 | 53,59% | 46,41% | 60,13% | 39,87% |
| 4 | 54,02% | 45,98% | 72,65% | 27,35% |
| 5 | 0,00% | 100,00% | 97,86% | 2,14% |
| 400 | ||||
| 1 | 50,10% | 49,90% | 40,17% | 59,83% |
| 2 | 52,51% | 47,49% | 48,50% | 51,50% |
| 3 | 52,31% | 47,69% | 58,78% | 41,22% |
| 4 | 48,34% | 51,66% | 69,53% | 30,47% |
| 5 | 0,00% | 100,00% | 97,36% | 2,64% |
| 500 | ||||
| 1 | 48,49% | 51,51% | 39,28% | 60,72% |
| 2 | 50,79% | 49,21% | 47,34% | 52,66% |
| 3 | 52,02% | 47,98% | 57,25% | 42,75% |
| 4 | 52,11% | 47,89% | 68,84% | 31,16% |
| 5 | 0,00% | 100,00% | 97,35% | 2,65% |
| 600 | ||||
| 1 | 47,69% | 52,31% | 44,24% | 55,76% |
| 2 | 47,64% | 52,36% | 53,09% | 46,91% |
| 3 | 48,49% | 51,51% | 62,79% | 37,21% |
| 4 | 47,60% | 52,40% | 73,60% | 26,40% |
| 5 | 0,00% | 100,00% | 98,43% | 1,57% |
| 700 | ||||
| 1 | 47,09% | 52,91% | 43,58% | 56,42% |
| 2 | 47,52% | 52,48% | 52,16% | 47,84% |
| 3 | 49,31% | 50,69% | 62,25% | 37,75% |
| 4 | 48,82% | 51,18% | 74,11% | 25,89% |
| 5 | 0,00% | 100,00% | 98,57% | 1,43% |
| 800 | ||||
| 1 | 44,25% | 55,75% | 45,19% | 54,81% |
| 2 | 46,73% | 53,27% | 52,02% | 47,98% |
| 3 | 46,67% | 53,33% | 60,71% | 39,29% |
| 4 | 46,94% | 53,06% | 73,27% | 26,73% |
| 5 | 0,00% | 100,00% | 98,92% | 1,08% |
| 900 | ||||
| 1 | 48,62% | 51,38% | 40,78% | 59,22% |
| 2 | 49,66% | 50,34% | 48,14% | 51,86% |
| 3 | 48,69% | 51,31% | 60,06% | 39,94% |
| 4 | 49,75% | 50,25% | 74,76% | 25,24% |
| 5 | 0,00% | 100,00% | 99,31% | 0,69% |
Ну тут все понятно. GB начиная с выборки в 300 тысяч примеров показывает 100% результат: все события 1 кидает в week=5, а для всех остальных раскидывает события поровну, в то время как нейросетка чего то пытается нащупать.
Таки дела
Что такое обучающая выборка назовите ее особенности
Наблюдения в обучающей выборке (training set) содержат опыт, который алгоритм использует для обучения. В задачах обучения с учителем каждое наблюдение состоит из наблюдаемой (зависимой) переменной и одной или нескольких независимых переменных.
Тестовое множество, или тестовая выборка, представляет из себя аналогичный набор наблюдений, который используется для оценки качества модели, используя некоторые показатели.
Важно, чтобы никакие наблюдения из обучающей выборки не были включены в тестовую выборку. Если тестовые данные действительно содержат примеры из обучающей выборки, то будет трудно оценить, научился ли алгоритм обобщать, используя обучающую выборку или же просто запомнил данные. Программа, которая хорошо обобщает, будет в состоянии эффективно выполнять задачи с новыми данными. И наоборот, программа, которая запоминит обучающие данные, создав чрезмерно сложную модель, может точно предсказывать значения зависимой переменной для обучающего множества, но не сможет предсказать значение зависимой переменной для новых примеров.
Переобучение
Запоминание обучающей выборки называется переобучением (overfitting). Программа, которая запомнит свои наблюдения не сможет выполнить поставленную задачу правильно, так как она запомнит отношения и структуры в данных, являющиеся шумом или простым совпадением. Балансировка между запоминанием и обобщением, или переобучением и недообучением (underfitting), является общей проблемой для многих алгоритмов машинного обучения. Одним из способов избежать переобучение для многих моделей является применение регуляризации.
Проверочное множество
В дополнение к обучающей и тестовой выборкам иногда требуется третий набор наблюдений, называемый проверочным (validation) множеством. Проверочное множество используется для настройки переменных, называемых гиперпараметрами, которые контролируют, как модель обучается. Программа по-прежнему оценивается на тестовом множестве, для получения оценки ее эффективности в реальном мире. Показатели эффективности на проверочном множестве не должны использоваться в качестве оценки реальной эффективности модели, так как программа была настроена, используя проверочные данные. Как правило, единая выборка наблюдений, используемых для обучения, разделяется на обучающее, тестовое и проверочное множества. Не существует каких-то особенных требований к размерам таких множеств, и они могут изменяться в соответствии с количеством имеющихся данных. На практике же, для обучающей выборки используется слудующая схема:
Качество данных
Некоторые обучающие выборки могут содержать только несколько сотен наблюдений, другие могут включать в себя миллионы точек данных. Недорогие облачные хранилища данных, множество встроенных в смартфоны и различные гаджеты датчиков внесли свой вклад в современное состояние BigData. У нас имеется доступ к обучающим множествам с миллионами, или даже миллиардами примеров. Предсказательная сила многих алгоритмов машинного обучения растет при увеличении размера обучающих выборок данных. Тем не менее, алгоритмы машинного обучения, также следуют принципу «мусор на входе — мусор на выходе». Студент, который готовится к экзамену, читая большой, запутанной учебник, который содержит много ошибок, скорее всего, не получит лучшую оценку, чем студент, который читает небольшой, но хорошо написанный учебник. Аналогично, алгоритм обучающийся на большой коллекции зашумленных, не относящихся к делу, или неправильно маркированных данных не будет работать лучше, чем алгоритм обучающийся на меньшем наборе данных, которые более адекватны задачам в реальном мире.
Многие из обучающих множеств подготавливаются вручную, или же с использованием полуавтоматических процессов. Создание больших коллекций данных для обучения по прецедентам может быть достаточно затратным процессом в некоторых областях.
Кросс-валидация
| A | B | C | D | E | |
| Перекрестная проверка, 1 итерация | Тестовое множество | Обучающее множество | Обучающее множество | Обучающее множество | Обучающее множество |
| Перекрестная проверка, 2 итерация | Обучающее множество | Тестовое множество | Обучающее множество | Обучающее множество | Обучающее множество |
| Перекрестная проверка, 3 итерация | Обучающее множество | Обучающее множество | Тестовое множество | Обучающее множество | Обучающее множество |
| Перекрестная проверка, 4 итерация | Обучающее множество | Обучающее множество | Обучающее множество | Тестовое множество | Обучающее множество |
| Перекрестная проверка, 5 итерация | Обучающее множество | Обучающее множество | Обучающее множество | Обучающее множество | Тестовое множество |
Оригинальный набор данных разбивается на пять подмножеств одинакового размера, обозначенных от A до E. Сначала модель обучается на частях В-Е, и тестируется на части данных А. На следующей итерации, модель обучается на разделах A, C, D и Е и тестируется на данных части В. Части меняются до тех пор, пока модель не обучится и протестируется на всех частях. Кросс-валидация дает более точную оценку эффективности модели, чем тестирование с использованием только одной части данных.